二进制中1的个数

前言

有一个整数，想知道它的二进制表示中有多个1，你会怎么做？本文将带大家深入学习下二进制以及它的各种运算，一步步的研究出这个问题的解决方案，欢迎各位感兴趣的开发者阅读本文。

前置知识

在解决这个问题之前，我们需要先了解下什么是二进制。

二进制

在计算机的世界里，只有0和1，也就是二进制。

符号数

在二进制中，数被分为有符号数和无符号数。

对于有符号数而言，符号的正、负机器是无法识别的，但由于“正、负”恰好是两种截然不同的状态，如果用“0”表示正，用“1”表示“负”，这样符号也被数字化了，并且规定将它放在有效数字的前面，即组成了有符号数。

因此，在二进制中使用最高位来表示符号。

• 最高位是0，表示正数。
• 最高位是1，表示负数。

二进制的最高位就是其第一位，例如：10000001100，它的最高位就是1。

对于无符号数而言，它表示的数其范围都是正数，所有位都用于表示数的大小。

有符号数的性质

对于有符号数而言，它有6个性质：

• 二进制的最高位是符号位：0表示正数，1表示负数
• 正数的原码、反码、补码都一样
• 负数的反码 = 它的原码符号位不变，其它位取反（0 -> 1; 1 -> 0）
• 0的反码、补码都是0
• 负数的补码 = 它的反码 + 1
• 在计算机运算的时候，都是以补码的方式来运算的

原码、反码、补码

上述性质中，我们提到了原码、反码、补码，接下来我们来学习下他们究竟是什么样的数字。

• 原码，分为两种情况：
  • 一个正数，按照绝对值大小转换成的二进制数
  • 一个负数，按照绝对值大小转换成的二进制数，然后最高位补1
• 反码，也分为两种情况：
  • 一个正数，它的反码与它的原码是相同的
  • 一个负数，它的反码为该数的原码除符号位外，各位取反
• 补码，也分为两种情况：
  • 一个正数，它的补码与它的原码也是相同的
  • 一个负数，它的补码为对该数的原码除符号位外各自取反后，在最后一位加1

进制转换

我们要对二进制进行运算，需要先将十进制数转为二进制，因此我们需要先学习下十进制转二进制的方法。

十进制转二进制

将十进制转为二进制主要分为三种情况：

• 正整数转二进制

计算规则为：除二取余(直至商为0)，然后倒序排列，高位补零。

知道规则后，我们举个例子，求一下80所对应的二进制数，如下图所示：

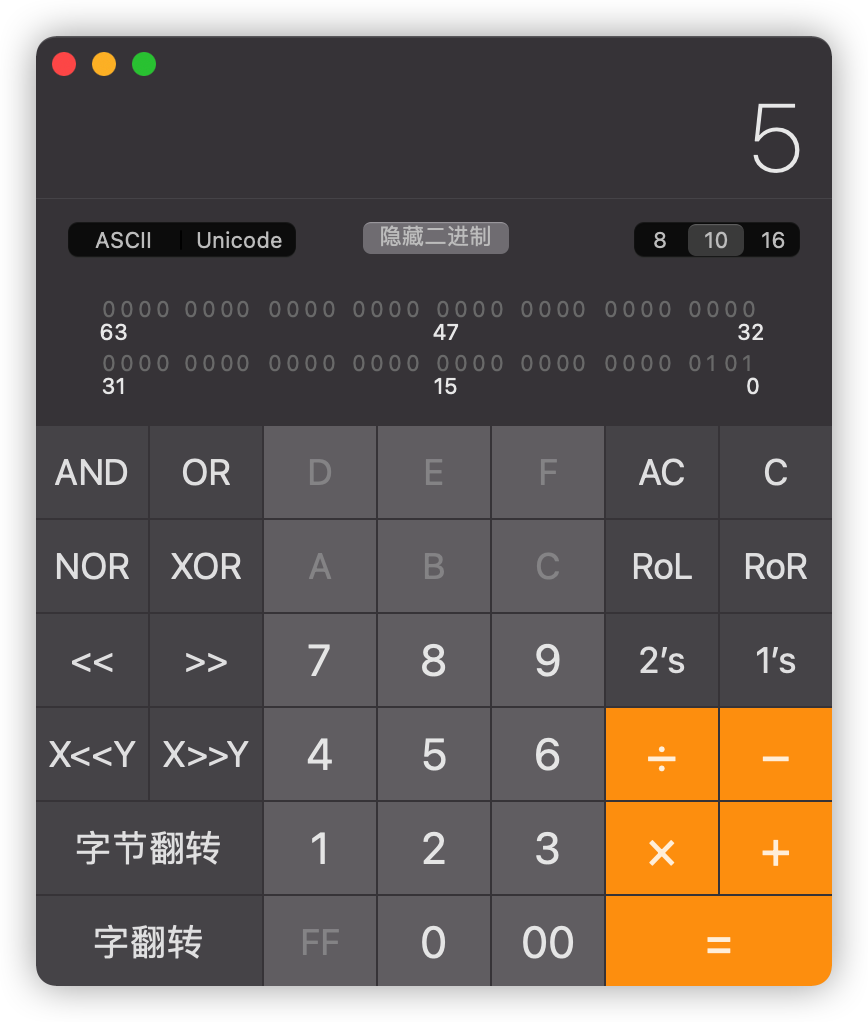
计算机内部表示数的字节单位是定长的（字长），如：8、16、32、64位。因此当计算出来的二进制的位数不够时，需要在高位进行补0。

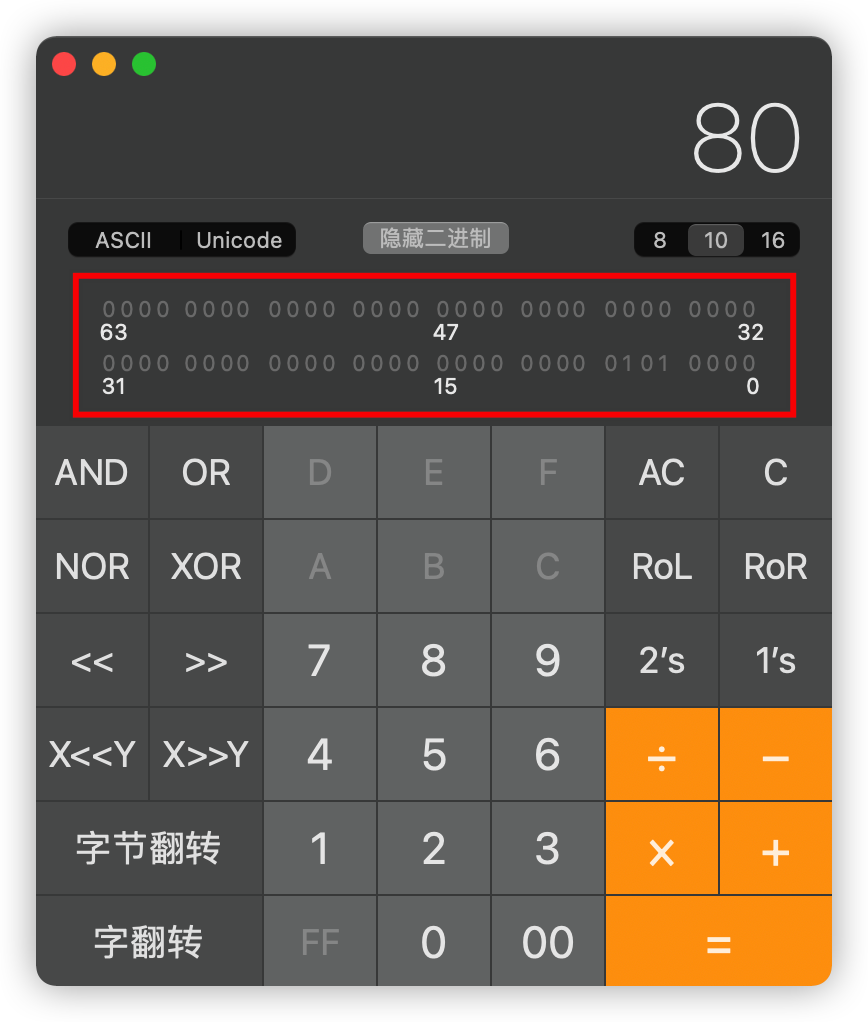
上述例子中，我们将80转为二进制数后，它的值为：1010000，字长为7，如果计算机的字长是64位，那么标准写法就是在它的最高位前面补57个0，我们用计算器来验证下，如下所示：

• 负整数转二进制

在计算机中，负数是以原码的补码形式进行表达的，通过前面的学习，我们知道了想求负数的补码，就得先求出它的原码。

我们以-80为例来计算下它的二进制码，步骤如所示：

1. 求原码，如下图所示：

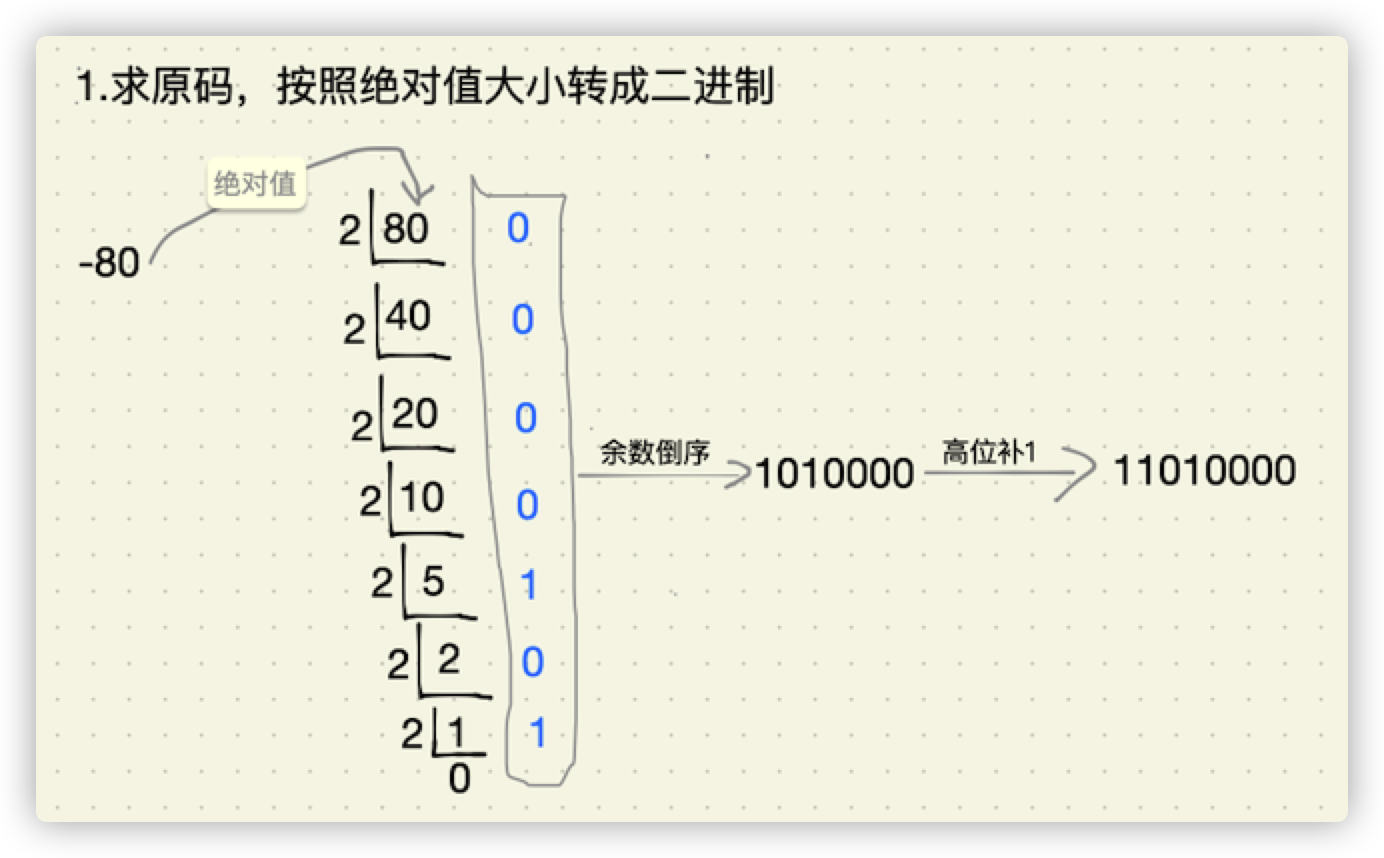
2. 求补码，如下图所示：

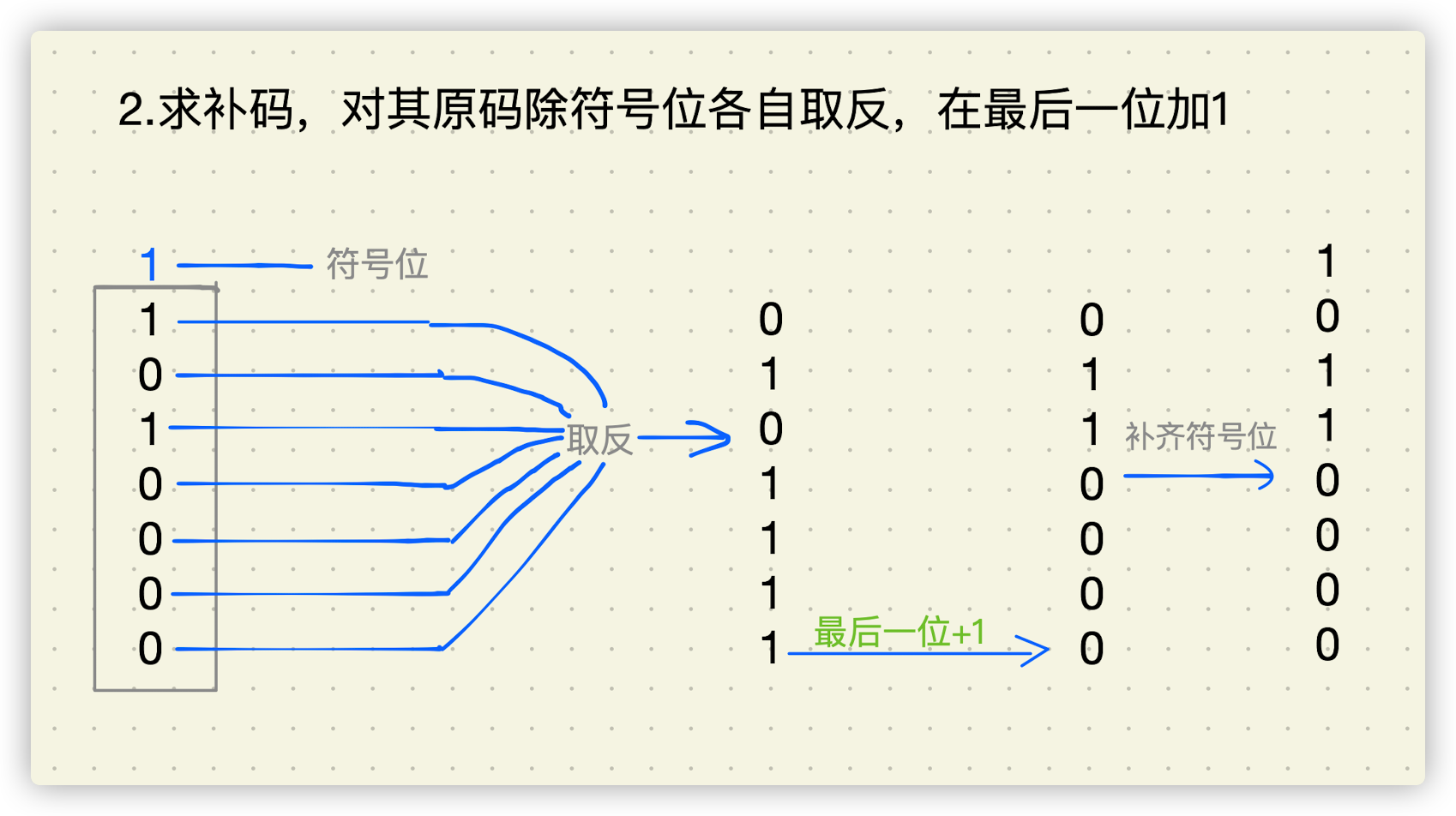
至此，我们得到了-80的二进制码：10110000

在正整数转二进制部分，我们讲了计算机是固定字长的，当计算出来的二进制位数不够时，正整数会在高位补0，负整数则会在高位补1。

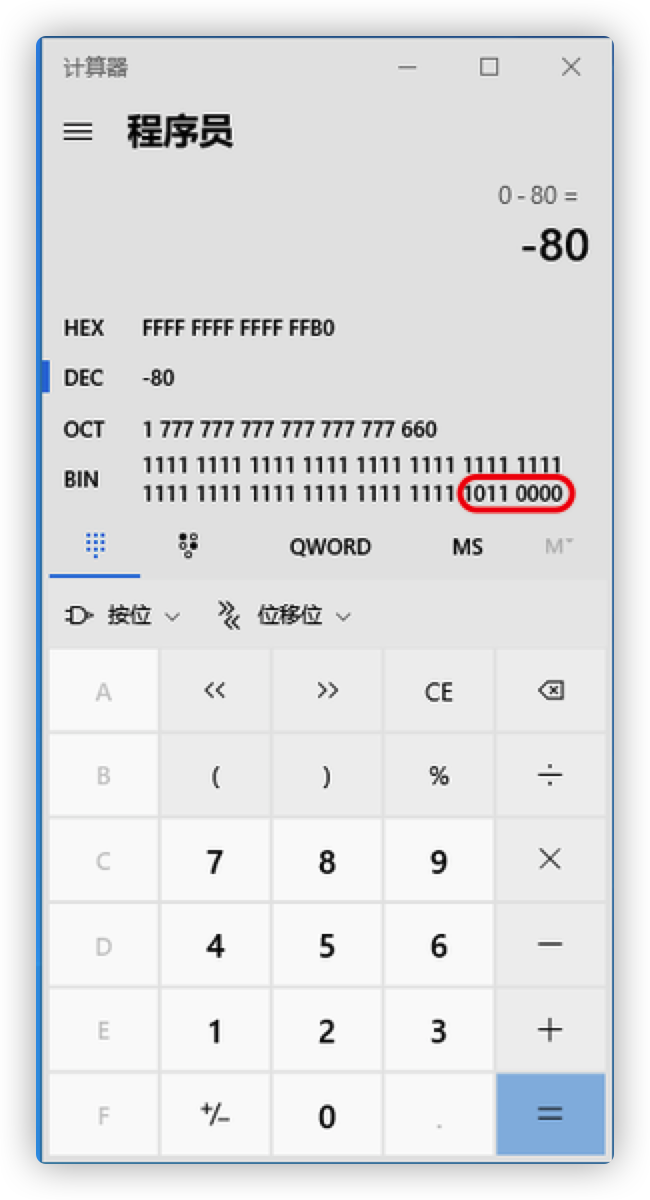
我们用计算器来验证下我们计算出来的-80的二进制码是否正确，如下所示：

• 小数转二进制

在二进制中，小数被称为浮点数，我们在将十进制小数转换为二进制小数时，需要以小数点为界限，将其拆分为整数部分和小数部分。

整数部分转为二进制，我们在前面已经讲过了（即除2取余）

小数部分转为二进制的方法为：乘2取整数部分，继续用小数部分乘2，直至小数部分为0（大多数情况下不会为0，需要确立精度）

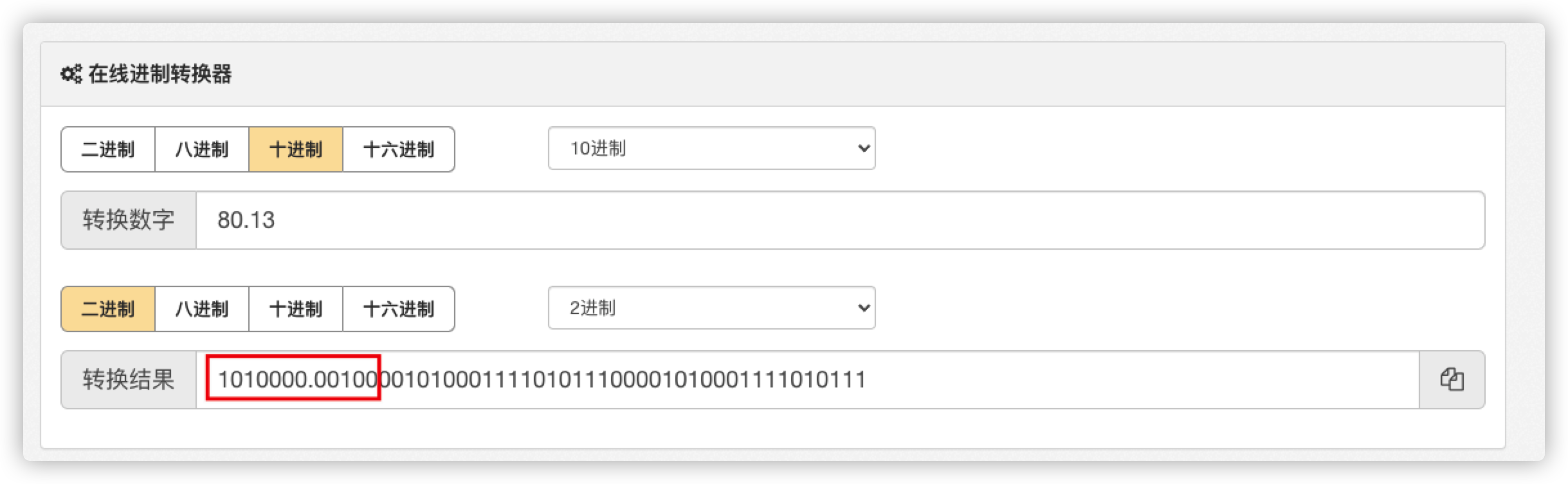
我们以80.13为例来计算下它的二进制码，如下图所示：

计算机中用二进制来表示小数时，大部分十进制小数都不能精确的用二进制来表示，当表示这种小数时，最大精确多少位，取决于计算机的字长。

上图中，我们计算出了80.13的二进制码为01010000.00100，我们精确到了小数点后5位。

我们用计算器来验证下是否正确。

二进制转十进制

同样的，二进制转十进制也分为三种情况：

• 正整数转十进制

从二进制的最低位开始，给每一位标上序号，取出不为0位置的数的序号，将其作为2的次方进行计算，最后将结果相加。

我们以01010000为例，求一下它的十进制数，如下图所示：

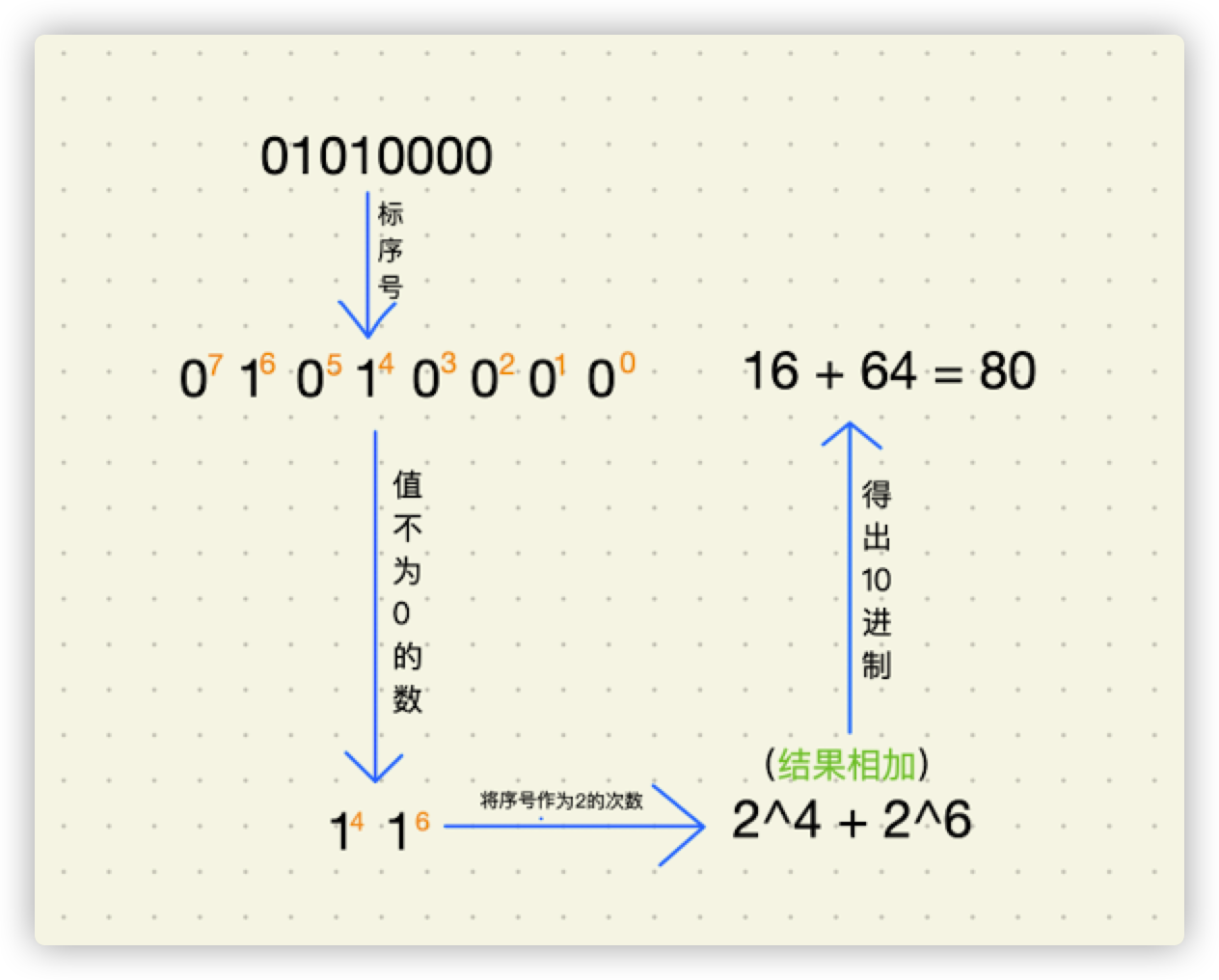
• 负整数转十进制

前面我们学习了十进制负整数转二进制的方法，那么二进制转十进制，则需要倒着来算，我们以10110000为例，步骤如下所示：

1. 根据补码求原码

2. 除去符号位，对其他位按照正整数转二进制的规则进行计算，最后补上负号，如下图所示：

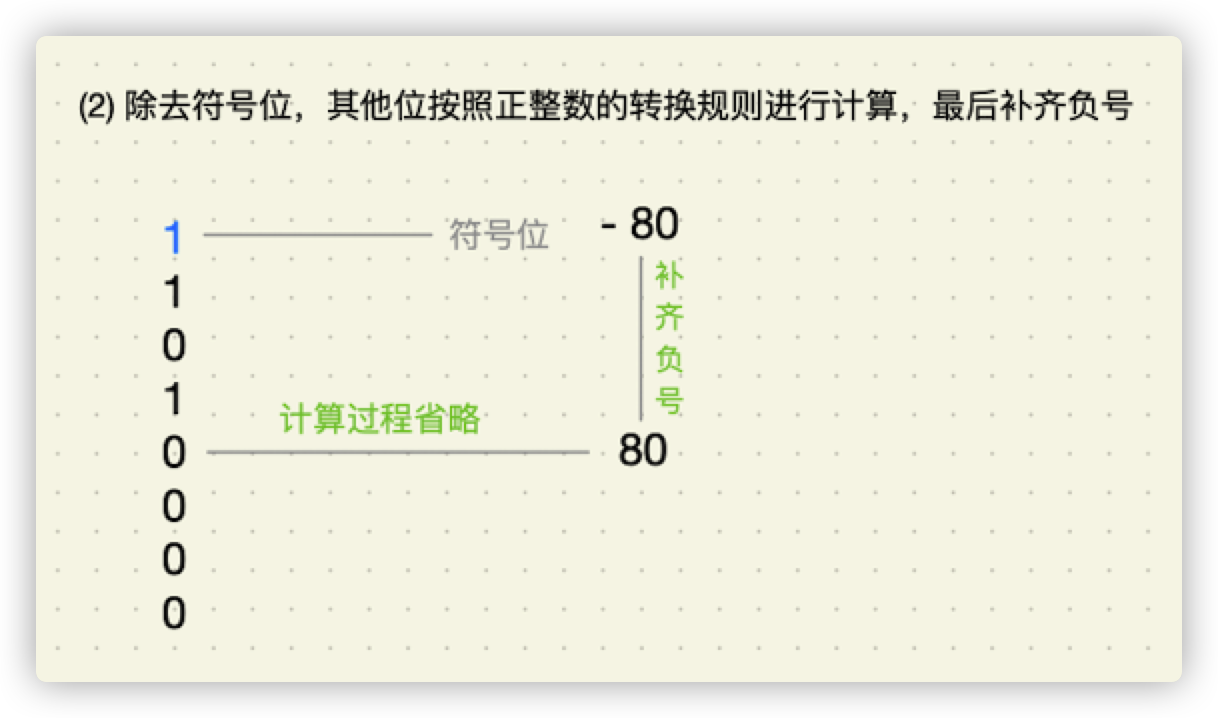
• 小数转十进制

给小数点后每一位标上负序号（从-1开始），取出不为0位置的数的序号，将其作为2的次方进行计算，最后将结果相加。

我们以01010000.00100为例，求出它的十进制数，如下图所示：

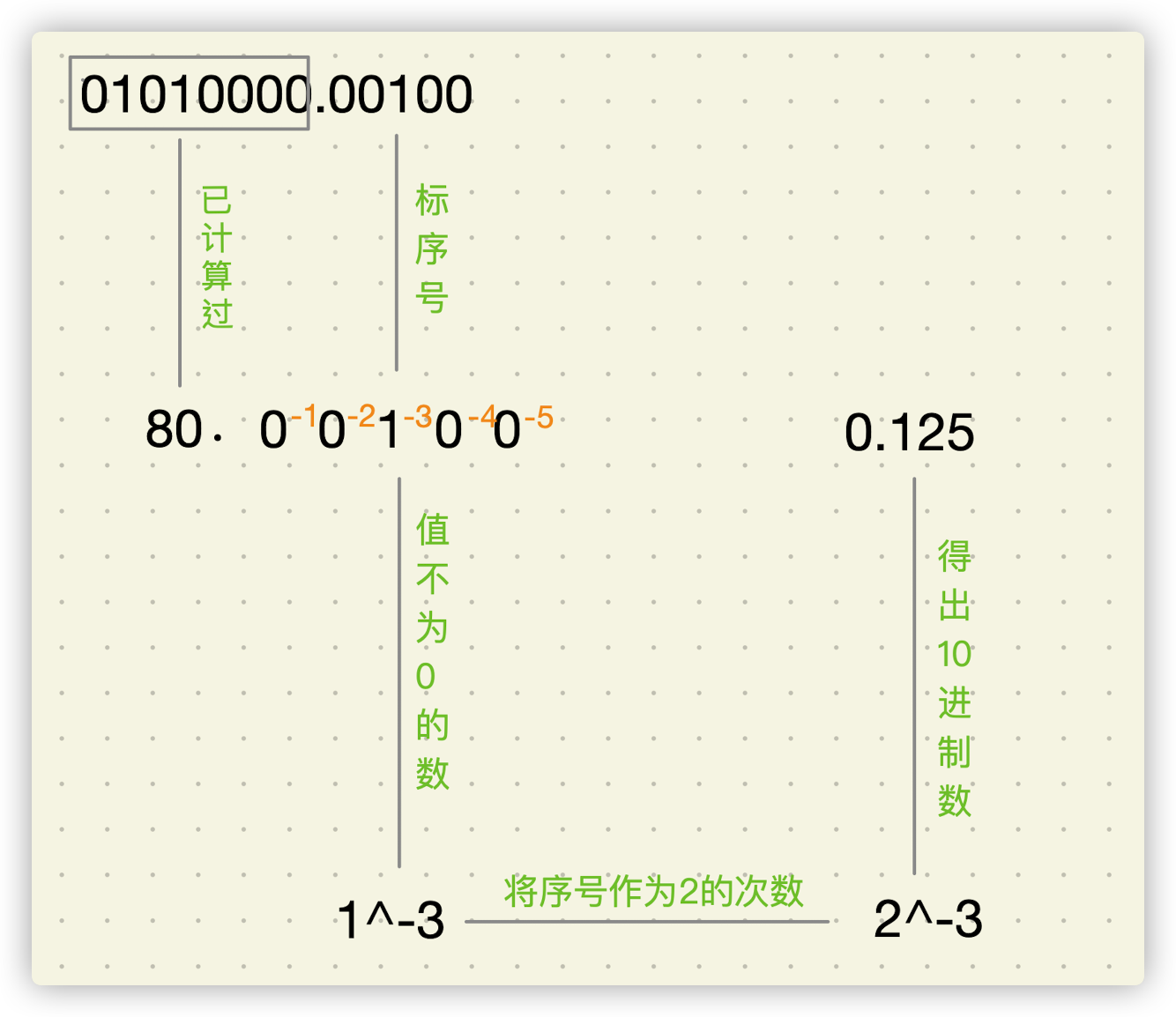
经过前面的学习，我们知道了十进制小数转二进制时，大多数情况是无法得到精确值的，我们用80.13举例时，精确到了小数点后5位。

同样的，我们将二进制小数转换为十进制数时，也是无法得到准确值的，最终值也取决于精度，此处我们保留2位小数，四舍五入后就为80.13。

有符号数的运算

了解完前置知识，接下来我们举几个例子来看下有符号数是如何进行运算的。

左移运算符

<<称为左移运算符，它的运算规则为：

• 移除二进制数最高位的0
• 在二进制数的末尾补上一个0

我们以01010000为例，假设他的字长为32位（多余的0省略），对其左移一位，它的运算过程如下图所示：

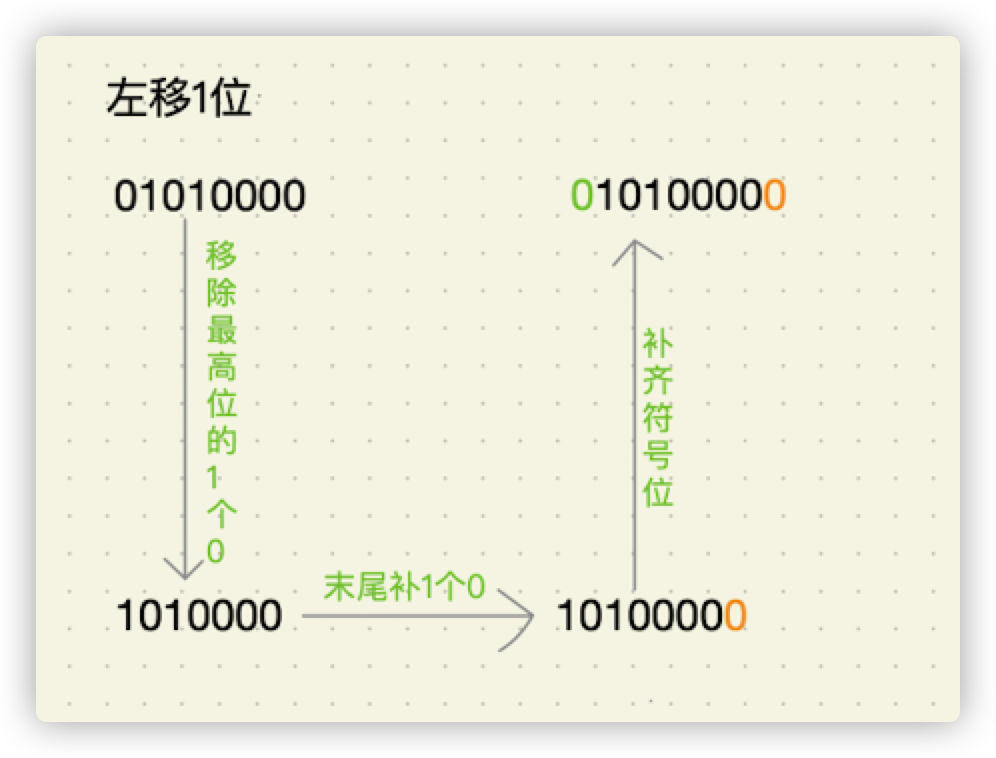
左移1位后，我们计算出来的结果为：010100000，转换成十进制后结果为2^5 + 2^7 = 32 + 128 = 160。

01010000的十进制数为80，左移动1位后，值变为了160，经过观察后，我们发现左移后的值正好是原值的2倍，等价于乘2操作。

大多数情况下我们可以将其当作乘2使用，但在一些特殊情况下它并不代表真正的乘2，例如，我们需要将其左移25位，如下图所示（我们把省略的0补上）：

左移25位后，我们发现它左侧的0已被删完，最高位变成了1，这个数也从原来的正数，变为了负数。如果我们左移26位，左侧的0不够，会开始从右侧取值，最终的值又变成了正数。

因此，我们会发现这样一条规律：

• 当左移的位数，超过剩余字长时，它的值并非乘2

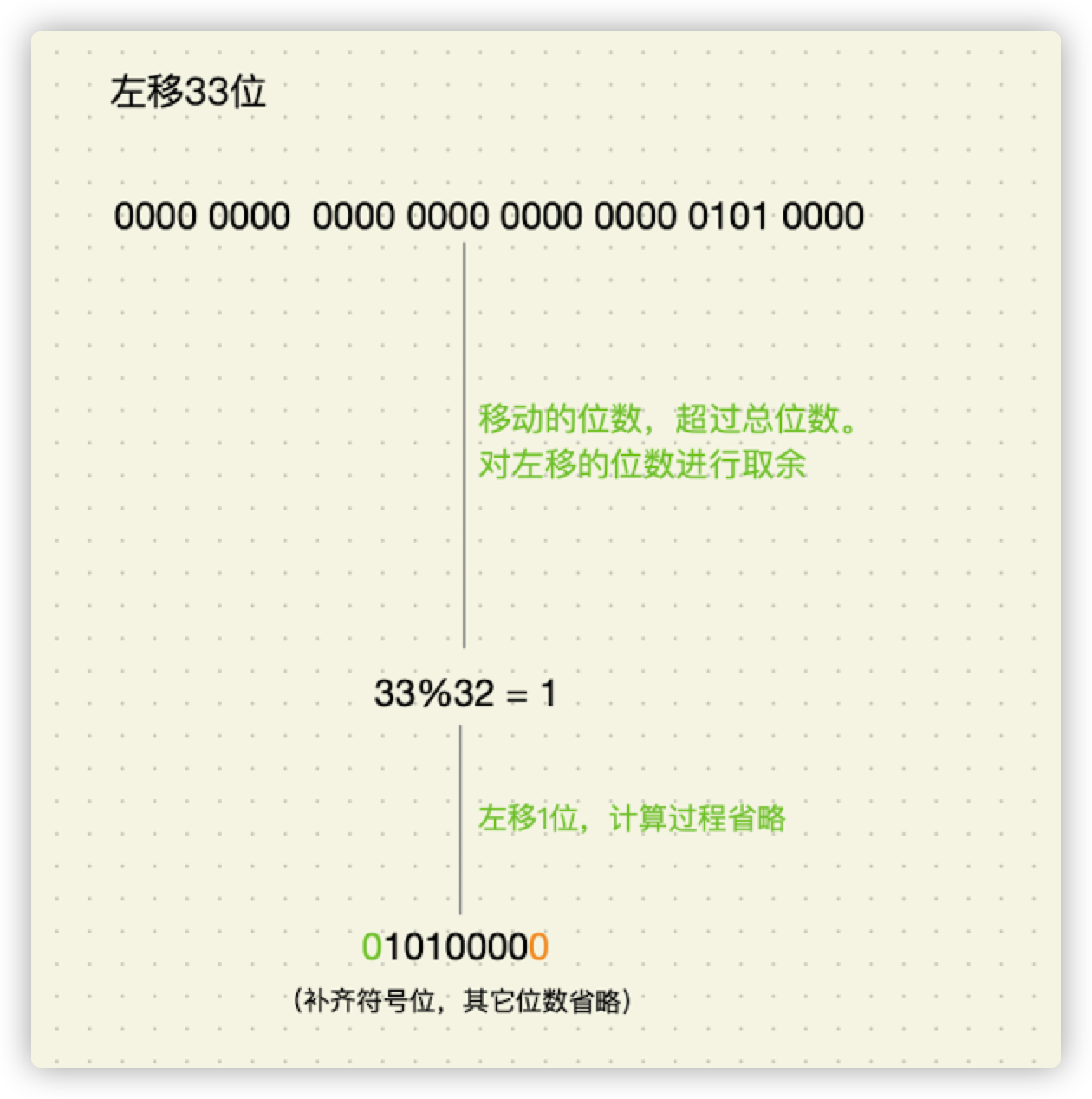
注意：如果任意一个二进制数，左移的位数大于等于字长（例如字长为32，我们左移32位，右边补32个0），那么与之对应的十进制数岂不是都为0了？

当然不是，二进制数进行左移时，当移动的位数大于等于它的字长时，位数会先求余数，然后再进行左移。

例如：我们需要对一个字长为32位的二进制数进行左移32位，那么就需要先求它的余数，即：32 % 32 = 0，需要左移0位。左移33位的值和左移1位是一样的。

右移运算符

>>称为右移运算符，它的运算规则分为正数与负数两种情况。

正数：

移除最低位的数，在最高位补0。

我们以01010000为例（十进制值为80），对其右移4位，计算过程如下图所示：

计算出来的二进制结果为00101，将其转位十进制，结果为：2^0 + 2^2 = 1 + 4 = 5,即：80 >> 4 = 5

我们用计算器来验证下：

负数：

经过前面的学习，我们知道了负数是以原码的补码形式存储的，它的右移规则为：

• 对补码进行右移，在最高位补1
• 求出其反码
• 对反码+1，求出原码

我们以10110000为例（十进制为-80），将其右移4位，计算过程如下所示：

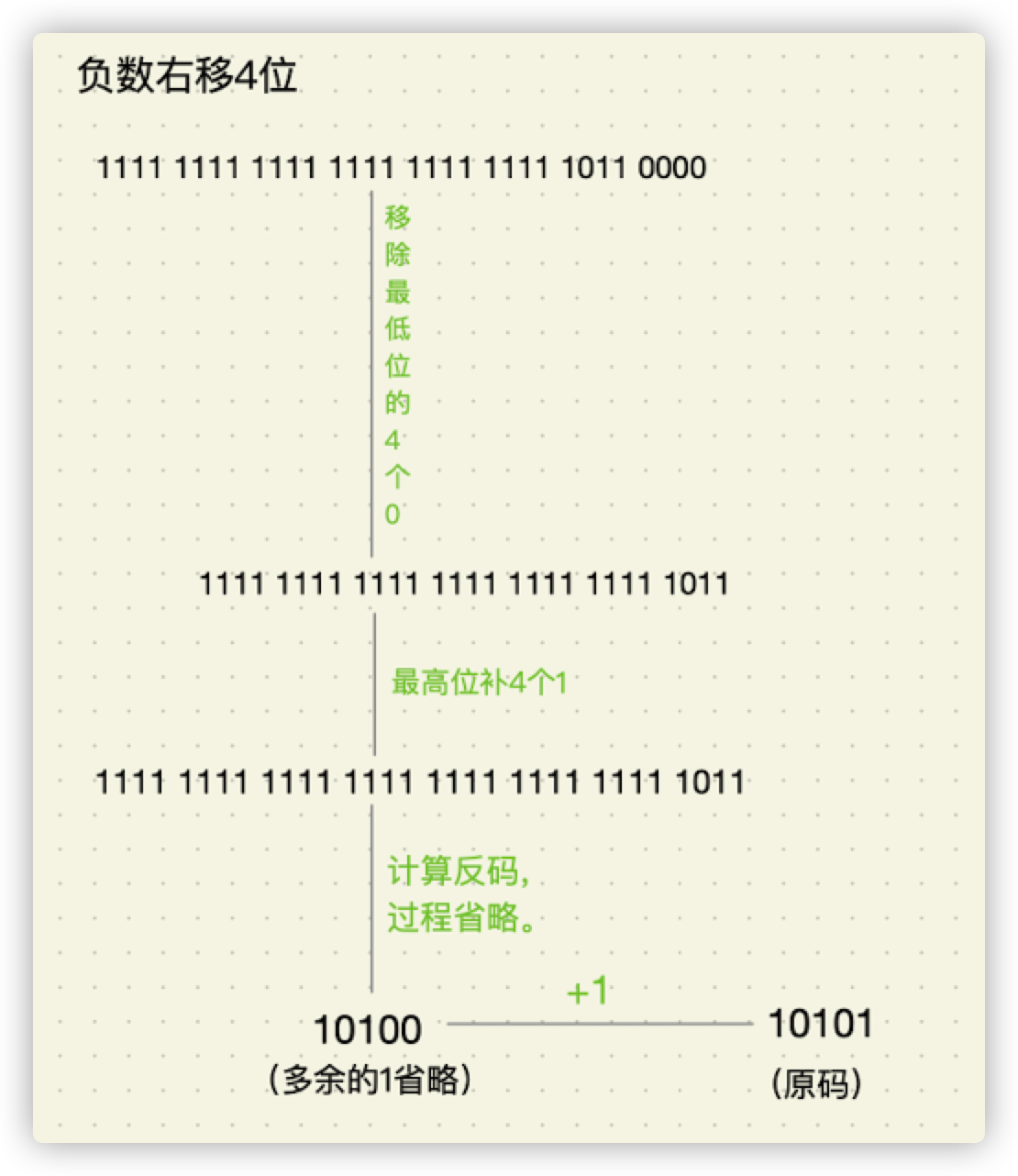
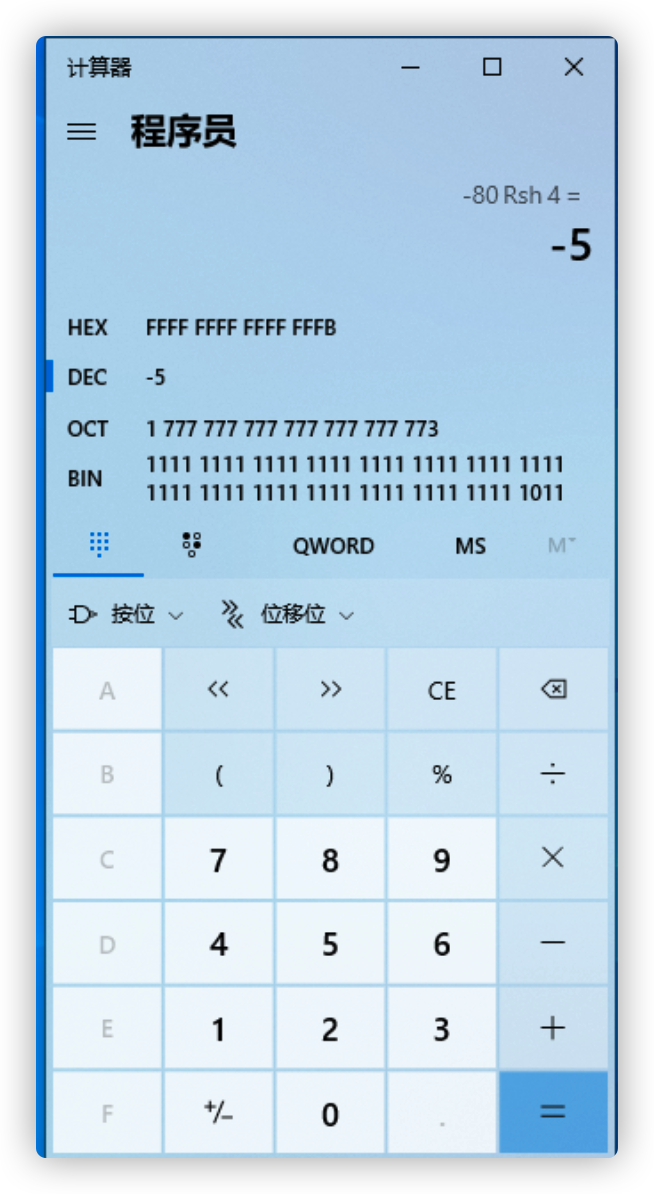
计算出来的二进制结果为11100,我们将其专为十进制：2^0 + 2^2 = 1 + 4 = 5，补齐符号位，结果为: -5。即：-80 >> 4 = -1。

我们用计算器来验证下，如下图所示：

与运算符

&称为与运算符，它的运算规则为：

• 符号左右两侧的数同时为1，结果就为1，否则为0

即：0 & 0 = 0; 0 & 1 = 0; 1 & 0 = 0; 1 & 1 = 1

接下来，看个十进制的例子，来看下它的运算过程，如下所示：

15 & 13，它的运算步骤为：

• 将十进制转为二进制
• 对二进制进行与运算

运算过程如下图所示：

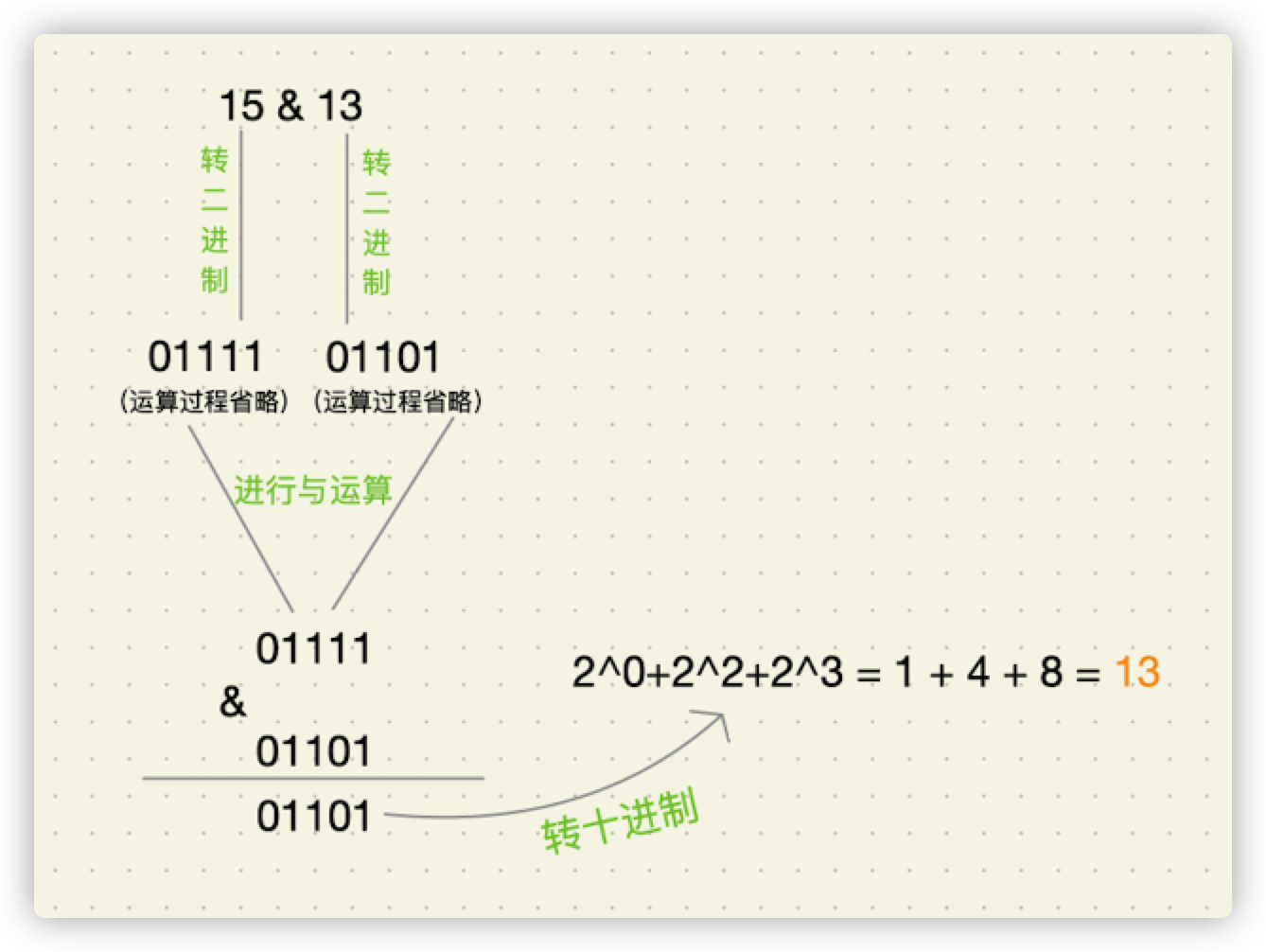
或运算符

|称为或运算符，它的运算规则为：

• 符号左右两侧的数，有一个为1，其值就为1

即：0 | 1 = 1; 1 | 0 = 1; 0 | 0 = 0; 1 | 1 = 1

我们继续以前个章节的数字为例，来看下15 | 13的运算步骤：

• 将十进制转二进制
• 对二进制进行或运算

运算过程如下图所示：

异或运算符

^称为异或运算符，它的运算规则为：

• 符号左右两侧的数，值不同，则该位结果为1，否则为0

即：0^0=0; 0^1=1; 1^0=1; 1^1=0

我们继续以15和13为例，看下15^13的运算步骤：

• 将十进制转二进制
• 对二进制进行异或运算

运算过程如下图所示：

问题求解

有了上述知识做铺垫后，接下来我们进入正题：有一个十进制整数，求它的二进制数中1的个数。

分析

在解决这个问题之前，我们先来分析这样一个场景：

如果一个整数不等于0，那么该整数的二进制表示中至少有一位是1。

先假设这个数的最右边一位是1，那么减去1时，最后一位变成0而其他所有位都保持不变。也就是最后一位相当于做了取反操作，由1变成了0。

接下来，假设这个数最右边的一位是0的情况：

如果该整数的二进制表示中，最右边的1，位于第m位，那么减去1时:

• 第m位由1变成了0

• 第m位之后的所有0都变成1

• 整数中第m位之前的所有位都保持不变

我们举个例子：

一个二进制数01010000，它的第4位是从最低位数起的第一个1，减去1后：

• 第4位变0
• 它后面的四个0全变1
• 它前面的所有位保持不变

因此得到的结果为01001111，转成十进制后为79。

结论

前面我们分析的两种情况中，我们发现把一个整数减去1，都是把最右边的1变成0。如果它的最右边还有0，则所有的0都变成1，而它左边的所有位都保持不变。

接下来，我们把一个整数和它减去1的结果做位与运算，相当于把它最右边的1变成0。我们还是以前面的01010000为例，它减去1的结果是01001111。我们再对它们二者进行位与运算，得到的结果是：01000000。

经过观察后，我们发现：把01010000最右侧的1变成了0，结果刚好就是01000000。

思路与编码

看到这里，我想各位开发者已经看出了此问题的解题思路了🤓。

没错，思路就是：把一个整数减去1，再和原整数做位与运算，会把该整数最右侧的1变成0。

那么，一个整数的二进制表示中有多少个1，就可以进行多少次这样的操作，直至整个数变为0，我们对每一次操作进行计数，就得到了这个问题的答案。

基于这种思路，我们就可以愉快的进行编码了，代码如下所示：

export default class BinaryOperation {
  /**
   * 获取二进制中1的个数
   * @param decimalVal 十进制数
   */
  public getBinaryOneNum(decimalVal: number): number {
    let count = 0;
    // 十进制数不为0，代表其二进制表示中仍存在1
    while (decimalVal !== 0) {
      // 二进制中所存在的1的总数+1
      count++;
      // 对十进制数与其-1后的数进行位与运算
      // 得出结果后替换原十进制数，进行下一轮计算，直至十进制数为0
      decimalVal = decimalVal & (decimalVal - 1);
    }
    // 返回结果
    return count;
  }
}

最后，我们写个测试用例，验证下上述代码能否正常工作，如下所示：

import BinaryOperation from "../BinaryOperation.ts";

const binaryOperation = new BinaryOperation();
const result = binaryOperation.getBinaryOneNum(80);
const result2 = binaryOperation.getBinaryOneNum(-80);
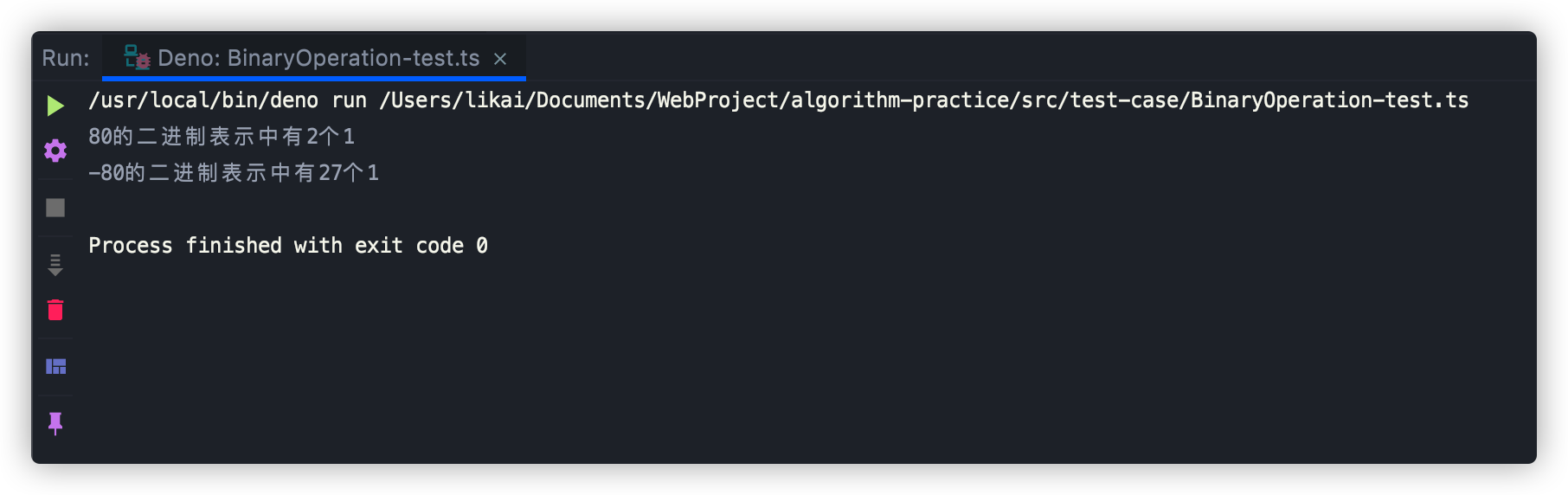
console.log(`80的二进制表示中有${result}个1`);
console.log(`-80的二进制表示中有${result2}个1`);

运行结果如下图所示：

示例代码地址：BinaryOperation.ts、BinaryOperation-test.ts

运行结果与我们手动算出来的二进制数中1的个数一致😋

-80我们在前面的章节中算过它的二进制表示为10110000，我们讲过二进制具体在计算机中占多少位，取决于它的字长，我们在书写时只需要标明它的符号位，高位上多出的1可以省略。

此处，我们算出-80的二进制表示中有27个1，我们加上此处的5个0，可以知道它的字长为27 + 5 = 32。

写在最后

至此，文章就分享完毕了。

我是神奇的程序员，一位前端开发工程师。

如果你对我感兴趣，请移步我的个人网站，进一步了解。

• 公众号无法外链，如果文中有链接，可点击下方阅读原文查看😊