前言
在JavaScript中有一个库函数(Math.pow())可以对一个数进行次方运算,本文将实现一个类似pow功能的函数,欢迎各位感兴趣的开发者阅读本文。
实现思路
第一眼看到这个问题,有些开发者可能思考几秒钟,觉得这很简单嘛。直接遍历次方数,将底数与前一次的计算结果相乘即可,直接一把梭🤓,很快就写完了代码,如下所示:
/**
* 计算一个数的次方
* @param base 底数
* @param exponent 指数
*/
public power(base: number, exponent: number): number {
let result = 1;
for (let i = 1; i <= exponent; i++) {
result *= base;
}
return result;
}
细心的开发者可能已经发现了这段代码的不足之处,上述代码只考虑了指数是正数的情况,当输入的指数为小于1的时候上述代码就计算错误了🌝
全面考虑的解法
接下来,我们把指数为负数和0时的情况考虑进去,来捋一下实现思路:
- 当指数为负数的时候,需要对指数求绝对值,算出次方的结果之后再取倒数
- 当指数为0时,我们就要考虑两种情况:
- 当底数为0且指数为负数时,就会出现对0求倒数,会导致程序运行出错,需要进行容错处理,将错误信息告知调用者
- 当底数为0且指数为0时,这在数学上是没有意义的,此处我们将结果返回0或1都可以
我们将上述思路转化为代码,如下所示:
/**
* 计算一个数的次方
* @param base 底数
* @param exponent 指数
*/
public power(base: number, exponent: number): number | string {
// 求出指数对绝对值
const absExponent = Math.abs(exponent);
// 程序会出错
if (base === 0 && exponent < 0) {
return "参数错误: 0的负次方不能进行计算";
}
// 当底数和指数都为0时,在数学上是没意义的
if (base === 0 && exponent === 0) {
return 0;
}
let result = 1;
for (let i = 1; i <= absExponent; i++) {
result *= base;
}
// 指数小于0, 对计算出的结果求倒数
if (exponent < 0) {
result = 1 / result;
}
return result;
}
我们将各种情况都考虑进去,作为参数传入上述代码,观察下运行结果,如下所示:
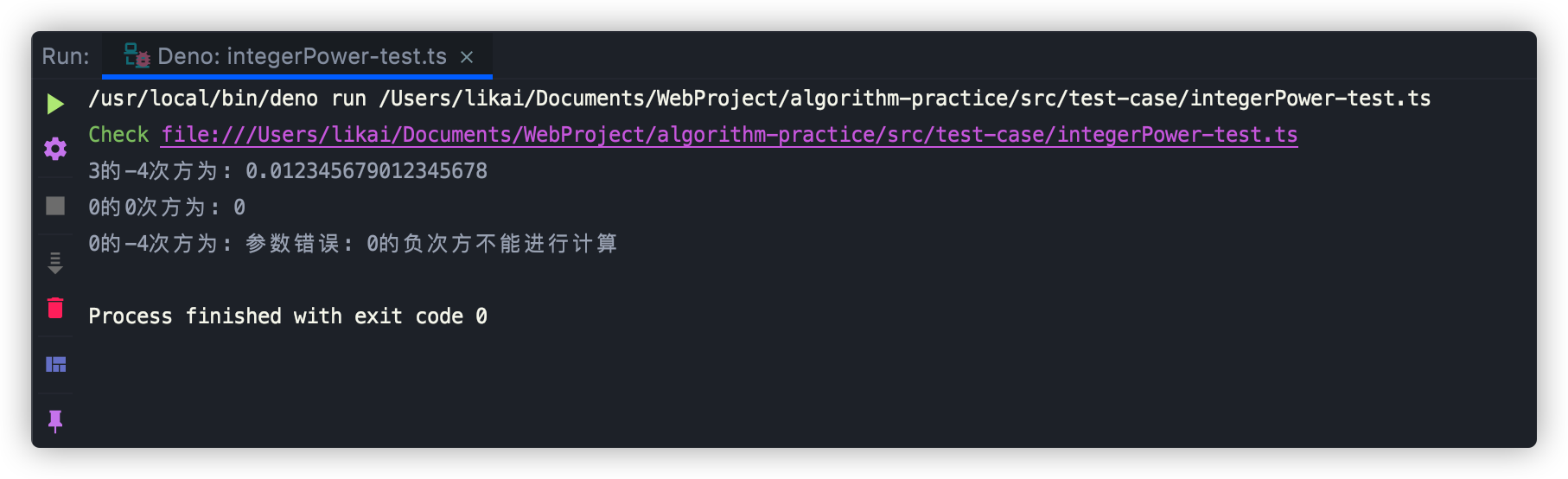
最优解
上述解法已经满足了题目要求,但是并不是最优解法,接下来,我们来看一种更好的解法。
上述代码中循环计算底数的指数次方代码可以拆分成一个函数,如下所示:
/**
* 求底数的指数次方
* @param base
* @param exponent
*/
private static powerWithExponent(base: number, exponent: number) {
let result = 1;
for (let i = 1; i <= exponent; i++) {
result *= base;
}
return result;
}
拆分后,我们考虑这样一个场景:
当指数为32时,就需要在上述函数的循环中做31乘法。然而,我们的目标就是求出一个数字的32次方,如果我们已经知道了它的16次方,那么只要在16次方的基础上再平方一次就可以了。而16次方是8次方的平方。
以此类推,我们求32次方只需要做5次乘法:
- 先求平方
- 在平方的基础上求4次方
- 在4次方的基础上求8次方
- 在8次方的基础上求16次方
- 在16次方的基础上求32次方
思考到这里,我们设要求的次方为n,那么:
- 当n为偶数时,可以拆分为
n/2 * n/2 - 当n为奇数时,可以拆分为
(n-1)/2 * (n-1)/2
乘式两边计算出结果后,仍然可以对结果应用上述规则进行计算,直至n为0或1,总结成公式后,如下图所示:
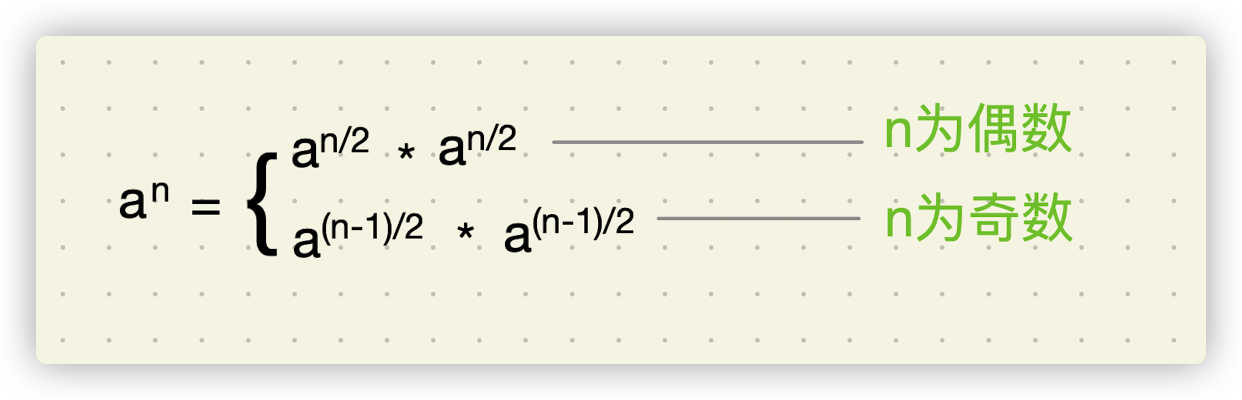
实现代码
有了公式后,我们很快就能想到可以用递归来解决这个问题,我们来画一下递归栈,如下图所示:
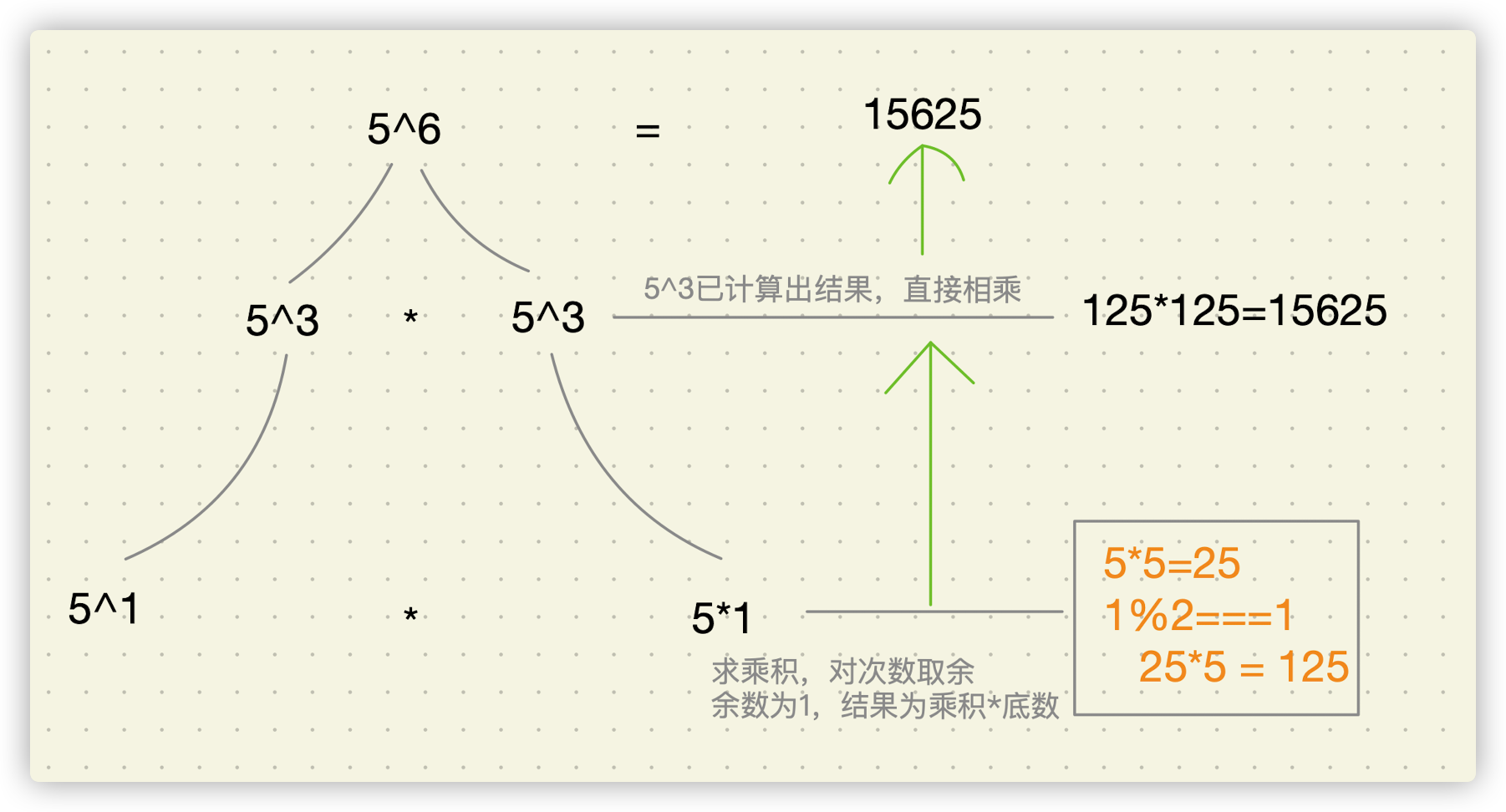
思路捋清楚后,就可以愉快的进入编码环节了🤓,完整代码如下所示:
export default class IntegerPower {
/**
* 计算一个数的次方
* @param base 底数
* @param exponent 指数
*/
public power(base: number, exponent: number): number | string {
// 求出指数对绝对值
const absExponent = Math.abs(exponent);
// 程序会出错
if (base === 0 && exponent < 0) {
return "参数错误: 0的负次方不能进行计算";
}
// 当底数和指数都为0时,在数学上是没意义的
if (base === 0 && exponent === 0) {
return 0;
}
// 进行次方运算
let result = this.powerWithExponent(base, absExponent);
// 指数小于0, 对计算出的结果求倒数
if (exponent < 0) {
result = 1 / result;
}
return result;
}
/**
* 求底数的指数次方
* @param base 底数
* @param exponent 指数
*/
private powerWithExponent(base: number, exponent: number): number {
// 递归终止条件
if (exponent === 0) {
// 非0数的0次方值为1
return 1;
}
if (exponent === 1) {
// 任意数的0次方为其本身
return base;
}
// 递归对指数/2,计算结果
// 用右移运算符代替除以2运算
let result =
this.powerWithExponent(base, exponent >> 1) *
this.powerWithExponent(base, exponent >> 1);
// 指数为奇数时,result就为result乘以底数
if (exponent % 2 === 1) {
result *= base;
}
return result;
}
}
上述代码中,我使用了右移运算符来代替除法运算,这样可以提升代码的执行速度。对此不了解的开发者请移步我的另一篇文章:二进制中一的个数-右移运算符
对递归不熟悉的开发者,请移步:递归的理解与实现
编写测试用例
接下来,我们将各种边界条件都考虑进去,验证下上述代码能否正确执行。
import IntegerPower from "../IntegerPower.ts";
const powerHandler = new IntegerPower();
const result1 = powerHandler.power(5, 6);
const result2 = powerHandler.power(3, -4);
const result3 = powerHandler.power(0, 0);
const result4 = powerHandler.power(0, 3);
const result5 = powerHandler.power(0, -3);
console.log(result1);
console.log(result2);
console.log(result3);
console.log(result4);
console.log(result5);
运行结果如下所示:
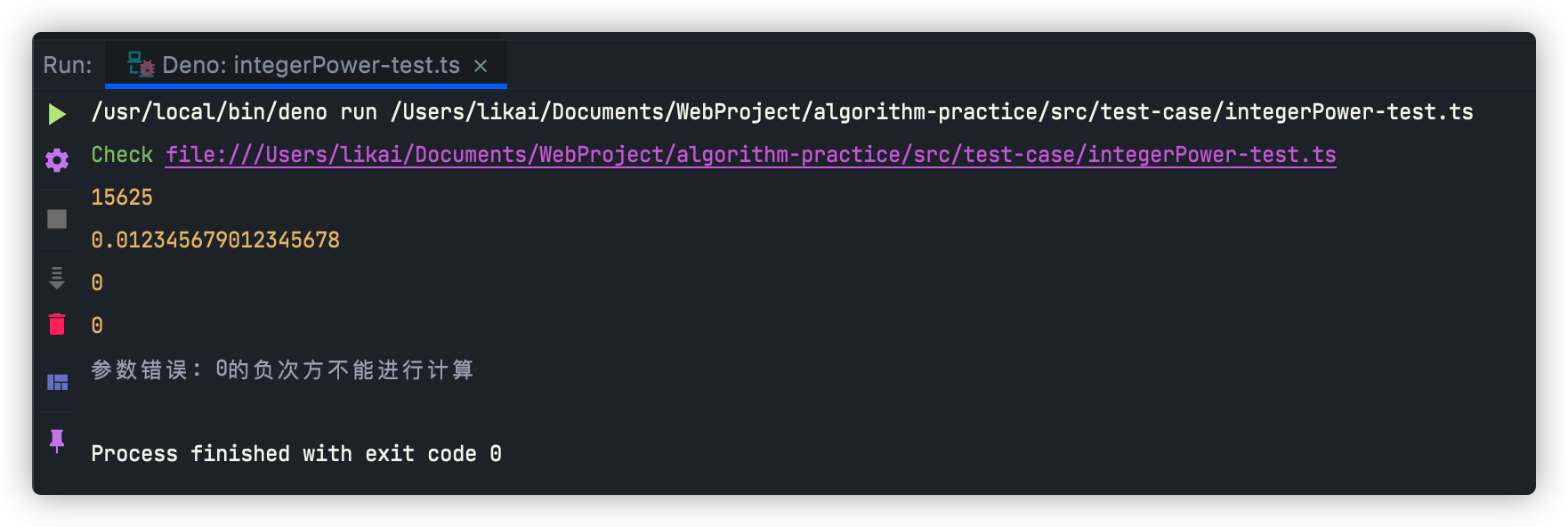
项目代码
文中的示例代码请移步:
写在最后
至此,文章就分享完毕了。
我是神奇的程序员,一位前端开发工程师。
如果你对我感兴趣,请移步我的个人网站,进一步了解。
- 文中如有错误,欢迎在评论区指正,如果这篇文章帮到了你,欢迎点赞和关注😊
- 本文首发于神奇的程序员公众号,未经许可禁止转载💌



评论区