前言
如果一个链表中包含环,如何找出环的入口节点?本文将分享一种解决方案,欢迎各位感兴趣的开发者阅读本文。
思路分析
我们通过一个例子来做进一步的分析:
- 准备一个有环链表,它包含6个节点,从头节点开始,其值依次为:1、3、8、9、12、18,末尾节点的下一个节点指向节点8。
- 获取该有环链表的环入口节点(即:节点8)
链表中是否有环
首先,我们需要确保链表中是否包含一个环,在上篇文章(获取链表中倒数第K个节点)中我们用双指针的思路解决了问题,那么,我们也尝试下能否用双指针来解决这个问题。
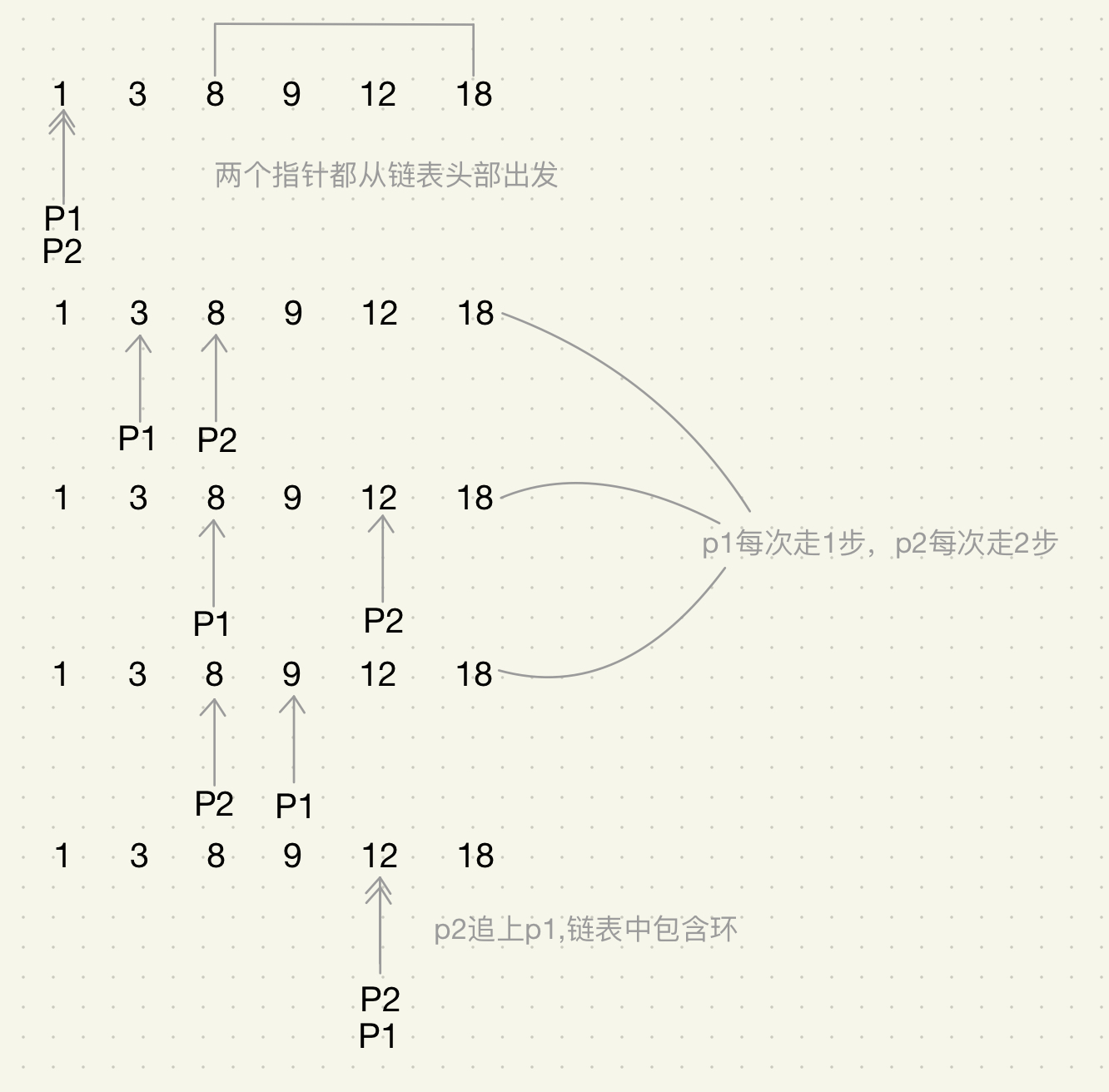
定义两个指针,从链表的头节点出发
- 第一个指针每次走一步,第二个指针每次走两步
- 走得快的指针追上了走得慢的指针,那么链表中就包含环
- 走得快的指针到了链表的末尾都没有追上第一个指针,那么链表就不包含环
寻找环的入口节点
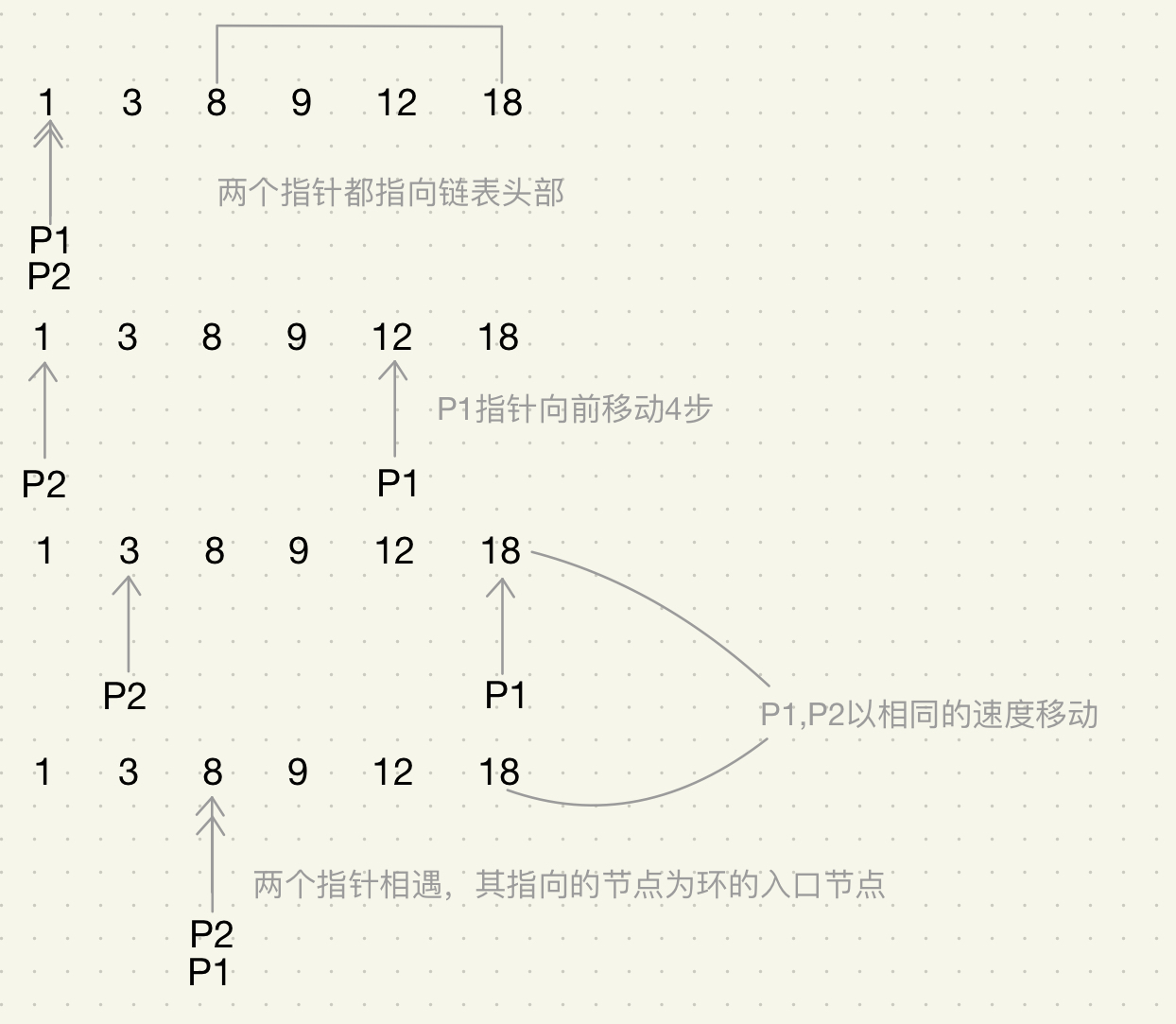
我们来观察下这个有环链表,将两个指针都指向链表头部。环中有4个节点,那么
- 将p1指针在链表上向前移动4步
- p1、p2指针以相同的速度在链表上向前移动
- 它们相遇的节点正好是环的入口节点
获取环中节点数量
通过上个章节的分析,我们知道了只要能得到环中的节点数量,就可以找到环的入口节点。在前面提到的判断一个链表中是否有环时用到了一快一慢两个指针。如果两个指针相遇,则表明链表中存在环。
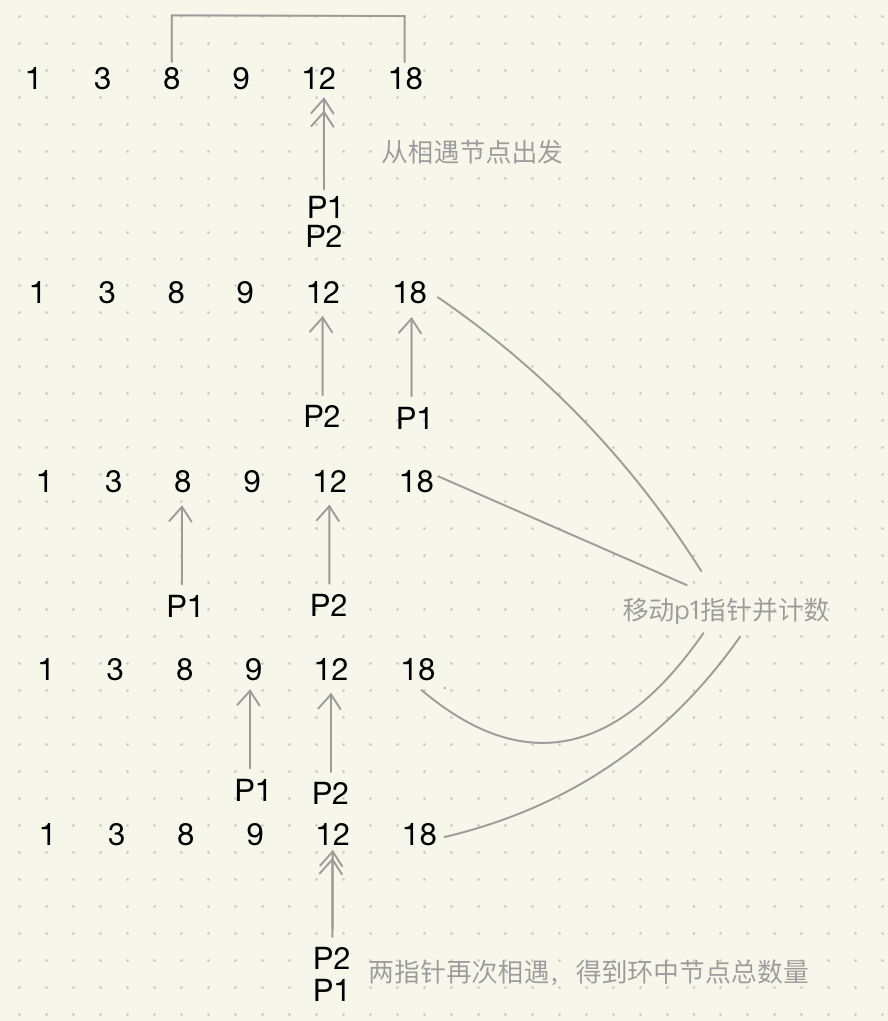
我们可以从它们相遇的节点出发,一边继续向前移动一边计数,当再次回到这个节点时,就可以得到环中节点数了。
- p1、p2指针指向判断链表中有环时的相遇节点
- p1指针继续向前移动,边移动边计数
- p1指针与p2指针再次相遇时,即可得到环中节点数量
实现代码
通过上面的分析,我们已经得到了解决问题的思路,接下来,我们来看下代码实现。
这里我们基于上篇文章所创建的类,扩展一个名为findRingEntranceNode的方法,实现寻找链表中环的入口节点函数:
- 初始化两个指针的指向至链表头部
- 判断链表中是否有环
- 移动p1、p2指针:p1指针每次走1步,p2指针每次走2步
- 若两个指针相遇,那么链表中就包含环。
- 若p1指针走到链表尾部都没有与p2指针相遇,那么链表中就不包含环
- 链表中有环,则做进一步的处理,获取环的入口节点
- 获取环中节点总数量
- 声明一个变量用于记录节点总数量
- p2指针不动,移动p1指针,每移动一次记录总数量的变量就自增一次
- p2、p1相遇时,变量所记录的值就是环中节点总数量
- 寻找环的入口节点
- 取出上一步得到的总数量,向前移动p1指针总数量步
- p1指针移动完毕后,重置p2指针的指向,将其指向链表头部
- p1、p2指针以相同的速度向前移动,两者相遇处正好是环的入口节点
- 获取环中节点总数量
// 寻找环的入口节点
findRingEntranceNode(): ListNode | null {
// 初始化两个指针指向
this.pNext = this.listHead;
this.pHead = this.listHead;
let hasRing = false;
while (this.pNext.next) {
// p1指针每次走1步
this.pNext = this.pNext.next;
// p2指针每次走2步
let step = 2;
while (this.pHead.next) {
if (step > 0) {
this.pHead = this.pHead.next;
step--;
}
if (step === 0) {
break;
}
}
// p1、p2相遇, 链表中就包含环
if (this.pNext === this.pHead) {
hasRing = true;
break;
}
}
// 链表中有环
if (hasRing) {
let ringCount = 0;
// 获取环中节点数量
while (this.pNext.next) {
ringCount++;
this.pNext = this.pNext.next;
// p1、p2相遇,得到环中节点总数量
if (this.pHead === this.pNext) {
break;
}
}
// 寻找环的入口节点
while (this.pNext.next) {
// 移动p1指针ringCount步
this.pNext = this.pNext.next;
ringCount--;
if (ringCount === 0) {
// 重置p2指针位置到链表头部
this.pHead = this.listHead;
break;
}
}
// p1、p2指针以相同的速度向前移动
while (this.pNext.next) {
this.pNext = this.pNext.next;
if (this.pHead.next) {
this.pHead = this.pHead.next;
}
// p1、p2相遇的节点正好是环的入口节点
if (this.pNext === this.pHead) {
return this.pNext;
}
}
return this.pNext;
}
// 链表中不存在环
return null;
}
完整代码请移步👉:GetLinkedListNode.ts
测试用例
接下来,我们将前言中的例子代入上个章节所实现的函数中,验证下它能否得出正确的结果。
const linkedList = new LinkedList();
linkedList.push(1);
linkedList.push(3);
linkedList.push(8);
linkedList.push(9);
linkedList.push(12);
linkedList.push(18);
// 修改最后一个节点的指针指向至链表的第3个节点,构造一个有环链表
linkedList.getElementAt(linkedList.size() - 1).next =
linkedList.getElementAt(2);
const getLinkedListNode = new GetLinkedListNode(linkedList.getHead());
resultNode = getLinkedListNode.findRingEntranceNode();
console.log("环的入口节点", resultNode);
运行结果如下所示,跟我们在思路分析章节中所得到的结果一致。
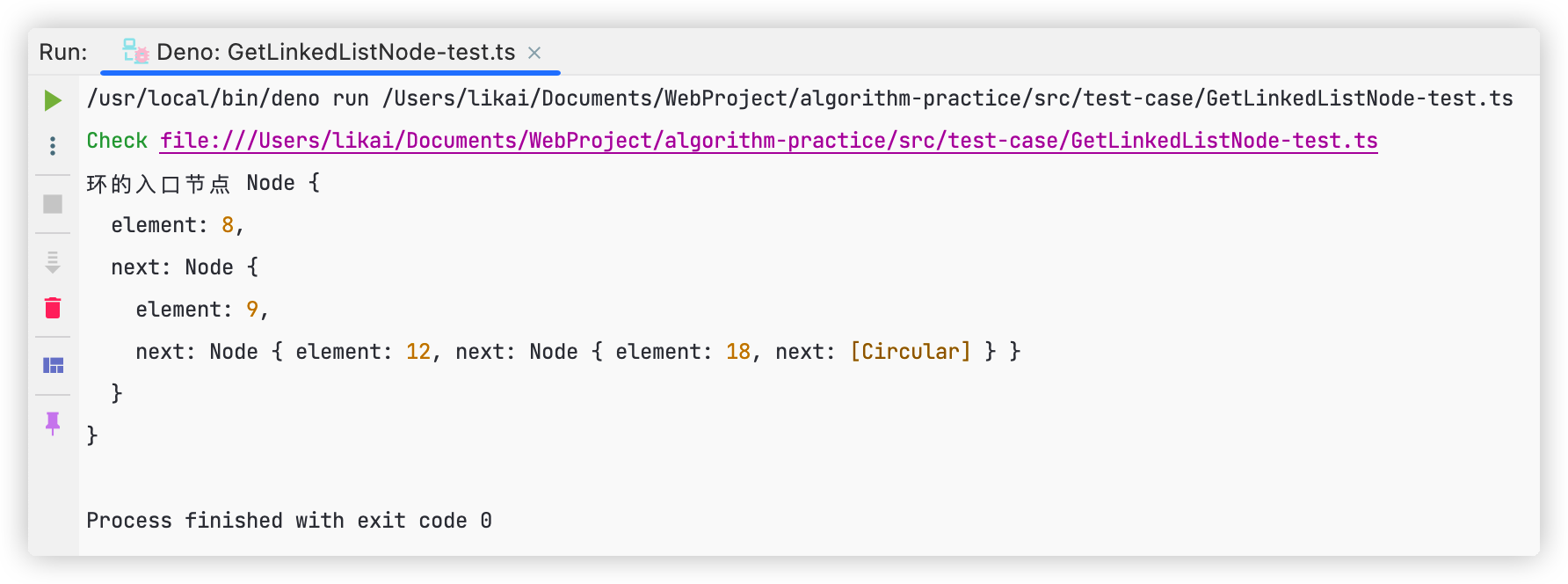
完整代码请移步👉:GetLinkedListNode-test.ts
注意:上述代码中用到的LinkedList是自定义的一个类,它实现了链表这个数据结构,对其原理感兴趣的开发者请移步我的另一篇文章👉:链表与变相链表的实现。
示例代码
本文所列举的代码,其完整版请移步👇:
写在最后
至此,文章就分享完毕了。
我是神奇的程序员,一位前端开发工程师。
如果你对我感兴趣,请移步我的个人网站,进一步了解。
- 文中如有错误,欢迎在评论区指正,如果这篇文章帮到了你,欢迎点赞和关注😊
- 本文首发于神奇的程序员公众号,未经许可禁止转载💌



评论区