前言
给定一个含有8个数字的数组,判断有没有可能把这8个数字分别放到正方体的8个顶点上,使得正方体上三组相对面上的4个顶点的和都相等。
本文就跟大家分享下这个问题的解决方案,欢迎各位感兴趣的开发者阅读本文。
正方体的组成
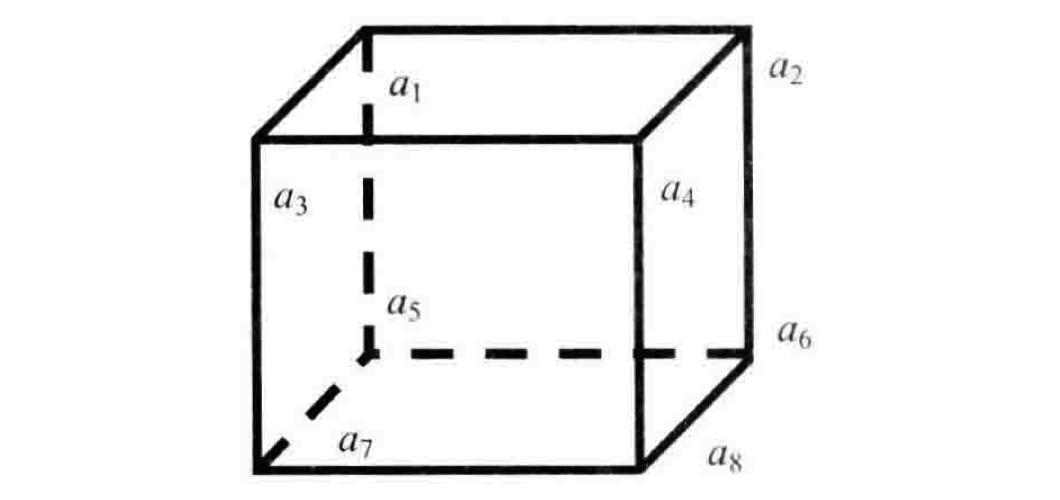
初次看到这个问题,很多开发者可能会比较蒙,一时间无法找到切入点。那我们就先画个正方体出来,给每个顶点标记a1, a2 ,a3 ,…, a8。如下图所示:
实现思路
有了图之后,我们在做进一步的分析,这个正方体有6个面,3组相对的面(上下、前后、左右):
- a1, a2, a4, a3 | a5, a6, a8, a7
- a1, a5, a6, a2 | a3, a4, a8, a7
- a1, a3, a7, a5 | a2, a4, a8, a6
有了这些条件后,再次结合题意,我们可知:只需要将8个数字分别放入正方体的8个顶点中,判断三组相对面的顶点和是否都相等,这个问题就解决了。
8个数字分别放到8个顶点上,所有数字都有可能放入任意一个顶点。换言之就是求这8个数字的所有排列,我的另一篇文章实现字符串的排列算法详细讲解了这个算法的实现思路,此处不过多赘述。
分析到这里,我们就得出了一个完整的实现思路:
- 求出给定数组中8个数字的所有排列
- 遍历所有排列,将每个排列中的元素映射到变量中(a1, a2, …, a8)
- 判断8个点组成的三组相对面的顶点和是否相等
实现代码
分析出思路后,我们就可以将上述思路转换成代码了,如下所示:
/**
* 能否构成正方体
* @param nums
*/
public isCubePossible(nums: Array<number>): boolean {
if (nums.length !== 8) {
return false;
}
// 获取8个点的所有排列
const list = this.permute(nums.join(""));
for (let i = 0; i < list.length; i++) {
// 将当前组合中的点转为number类型放入item
const item: Array<number> = [];
for (let j = 0; j < list[i].length; j++) {
item.push(+list[i][j]);
}
// 从当前组合中获取正方体的8个点
const [a1, a2, a3, a4, a5, a6, a7, a8] = item;
// 判断正方体三组相对面上的点相加是否相等
if (
a1 + a2 + a4 + a3 === a5 + a6 + a8 + a7 &&
a1 + a5 + a6 + a2 === a3 + a4 + a8 + a7 &&
a1 + a3 + a7 + a5 === a2 + a4 + a8 + a6
) {
return true;
}
}
return false;
}
上述代码中没有列举
permute方法的具体实现,对此感兴趣的开发者请移步:ArrayOfStrings.ts
八皇后问题
在一个8*8的棋盘上放置八个皇后,使得它们彼此之间不会互相攻击(即不在同一行、同一列或同一对角线上),总共有多少种摆法?如下图所示列举了其中一种摆法:

实现思路
分析题目后 ,我们知道了两个皇后不能处在同一行,那么肯定是每个皇后独占一行。那我们就先把皇后定义出来,用一个数组来表示皇后在棋盘上的列号,分别用0~7(棋盘上有8个皇后)对这个数组进行初始化。
棋盘上每一行所放置的皇后,它都可以放在这一行的任意位置。很显然,这也需要用到全排列求出它的所有放置组合。因为我们用的不同数字对数组进行的初始化,所以任意两个皇后肯定不同列。
因此,我们只需要判断每一组排列对应的8个皇后是不是在同一条对角线上,即:对于数组的两个下标i和j,是否有i-j === queens[i] - queens[j] || j-i === queens[j] - queens[i],这个问题就得到了解决。
我们来写一下实现思路:
- 定义皇后数组,分别用0~7对这个数组进行初始化
- 求出这个数组的所有排列
- 遍历所有排列,判断每一个排列是否满足不在同一对角线的条件
- 遍历满足条件的排列,对棋盘进行填充(将皇后放置在棋盘上)
实现代码
我们将上述思路转换为代码,如下所示:
public eightQueens(): Array<Array<Array<number>>> {
const queens = [0, 1, 2, 3, 4, 5, 6, 7];
const solutions: Array<Array<Array<number>>> = [];
// 获取所有组合
const list = this.permute(queens.join(""));
for (let i = 0; i < list.length; i++) {
// 求出的组合中元素值为string类型的,这里需要将其转为number类型
const item: Array<number> = [];
for (let j = 0; j < list[i].length; j++) {
item.push(+list[i][j]);
}
// 不在对角线上
if (this.isValidPlacement(item)) {
const solution: Array<Array<number>> = [];
// 遍历此组合,取出皇后的摆放位置
for (let j = 0; j < item.length; j++) {
const col = item[j];
const row: Array<number> = Array(8).fill(0);
row[col] = 1;
solution.push(row);
}
solutions.push(solution);
}
}
return solutions;
}
/**
* 判断当前组合是否满足排列要求(不在对角线上)
* @param queens
* @private
*/
private isValidPlacement(queens: Array<number>) {
for (let i = 0; i < queens.length; i++) {
for (let j = i + 1; j < queens.length; j++) {
if (Math.abs(queens[i] - queens[j]) === Math.abs(i - j)) {
// 在对角线上
return false;
}
}
}
return true;
}
测试用例
我们用一个例子来校验下上述代码能否正常执行。
const arrayOfStrings = new ArrayOfStrings();
console.log(
"能否构成正方体",
arrayOfStrings.isCubePossible([1, 2, 3, 4, 5, 6, 7, 8])
);
console.log("八皇后问题有", arrayOfStrings.eightQueens().length, "种摆法");

示例代码
本文用到的代码完整版请移步:
写在最后
至此,文章就分享完毕了。
我是神奇的程序员,一位前端开发工程师。
如果你对我感兴趣,请移步我的个人网站,进一步了解。
- 文中如有错误,欢迎在评论区指正,如果这篇文章帮到了你,欢迎点赞和关注😊
- 本文首发于神奇的程序员公众号,未经许可禁止转载💌



评论区