前言
本文将介绍两种算法设计技巧:贪心算法与回溯算法,并用TypeScript将其实现,欢迎各位感兴趣的开发者阅读本文。
贪心算法
贪心算法遵循一种近似解决问题的技术,期盼通过每个阶段的局部最优选择(当前最好的解),从而达到全局的最优。
实例讲解
接下来我们通过两个例子讲解下贪心算法。
最少硬币找零问题
最少硬币找零问题也可以用贪心算法来解决,大部分情况下的结果都是最优的,不过对于有些面额而言,结果不会是最优的。
实现思路
- 需要两个参数:硬币面额
coins、找零金额amount - 声明辅助变量
change,用于存储找零方案 - 声明辅助变量
total,用于存储当前已找零金额 - 从大到小遍历
coins- 取出当前遍历到的面额,判断当前取出的面额加上total,其值是否小于
amount - 如果小于等于,则执行while循环,将当前面额放入找零方案中,total的值加上当前面额
- 否则退出while循环,继续下一轮for循环,直至
coins被取完
- 取出当前遍历到的面额,判断当前取出的面额加上total,其值是否小于
- 循环结束,找零方案已计算完毕,返回找零方案
change
实现代码
接下里我们将上述思路转换为代码,我们继续使用上一篇文章中创建的DesignSkills.ts文件,在其中添加如下代码。
knapSackGreedy(capacity: number, weights: number[], values: number[]): number {
const n = values.length;
// 已装入背包的物品总重量
let load = 0;
// 已装入背包的物品总价值
let val = 0;
for (let i = 0; i < n && load < capacity; i++) {
// 物品可以完整的放入背包
if (weights[i] <= capacity - load) {
// 将物品的价值计入背包已装入物品的总价值
val += values[i];
// 将物品的重量计入背包已装入物品的总重量
load += weights[i];
} else {
// 物品无法完整的放入背包,计算能够装入部分的比例
const r = (capacity - load) / weights[i];
// 将计算出的物品价值计入背包已装入物品的总价值
val += r * values[i];
// 将物品的重量计入背包已装入物品的总重量
load += weights[i];
}
}
// 返回物品总价值
return val;
}
编写测试代码
我们通过一个例子来测试下上述代码能否正确执行
const designSkills = new DesignSkills();
const result = designSkills.minCoinChangeGreedy([1, 5, 10, 25], 8);
console.log(`找零方案: ${result}`);

背包问题
用动态规划只能解决整数背包问题,而贪心算法可以解决分数背包问题,我们使用动态规划中举的例子来看下分数背包问题。
如下所示:
| 物品 | 重量 | 价值 |
|---|---|---|
| 1 | 2 | 3 |
| 2 | 3 | 4 |
| 3 | 4 | 5 |
背包的容量为5,要将上述物品放进背包里,最佳方案是放入物品1和物品2,总重量为5,总价值为7。
使用贪心算法解决容量为5的背包,得到的结果是一样的,此处我们考虑背包容量为6的情况。
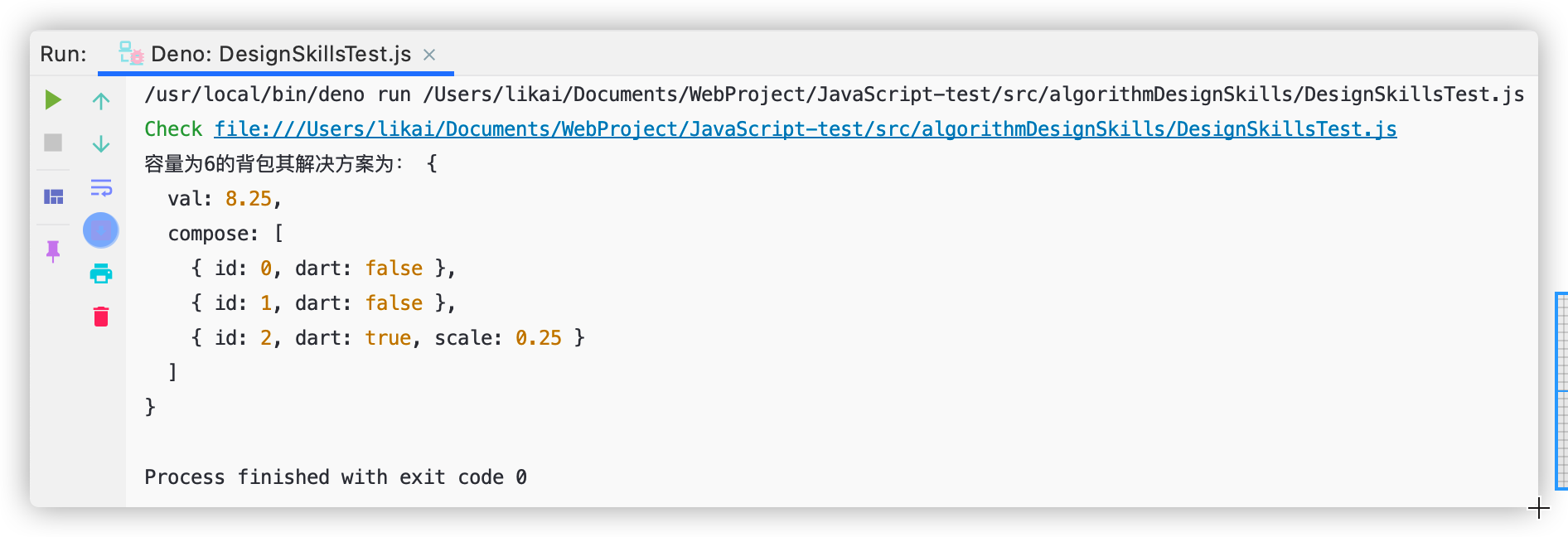
在这种情况下,解决方案是装入物品1和物品2,再装入25%的物品3,总价值为8.25。
实现思路
接下来,我们来看看如何用贪心算法解决上述分数背包问题。
- 需要3个参数:背包容量
capacity、物品重量weights、物品价值values - 声明三个辅助变量:物品数量
n、已装入背包的物品总重量load、已装入背包的物品总价值val。 - 遍历背包中的物品,终止条件为当前遍历到的元素小于
n且load小于capacity- 如果当前遍历到的物品重量
weights[i]小于等于背包容量capacity- 以装入背包的物品总量load,则代表物品可以完整的放入背包,将当前物品的重量和价值计入已装入背包中 - 否则,物品无法完整放入背包,计算能够装入部分的比例,计算方法为:(背包容量-已装入背包的物品总重量)/ 当前要放入背包的物品重量
- 用计算出来的比例*当前物品的价值,将得出的结果计入以装入背包的物品总价值中。将当前物品的重量的计入已装入背包的总重量中。
- 如果当前遍历到的物品重量
- 遍历结束,物品价值计算完毕,返回已装入物品总价值。
实现代码
接下来,我们将上述思路转换为代码。
/**
* 贪心算法: 背包问题
* @param capacity 背包容量
* @param weights 物品重量
* @param values 物品价值
*/
knapSackGreedy(
capacity: number,
weights: number[],
values: number[]
): { val: number; compose: ({ dart: boolean; scale: number; id: number } | { dart: boolean; id: number })[] } {
const n = values.length;
// 存储解决方案
const compose = [];
// 已装入背包的物品总重量
let load = 0;
// 已装入背包的物品总价值
let val = 0;
for (let i = 0; i < n && load < capacity; i++) {
// 物品可以完整的放入背包
if (weights[i] <= capacity - load) {
// 将物品的价值计入背包已装入物品的总价值
val += values[i];
// 将物品的重量计入背包已装入物品的总重量
load += weights[i];
// 当前物品可以完整放入,将物品编号放入组合方案中
compose.push({ id: i, dart: false });
} else {
// 物品无法完整的放入背包,计算能够装入部分的比例
const r = (capacity - load) / weights[i];
// 将计算出的物品价值计入背包已装入物品的总价值
val += r * values[i];
// 将物品的重量计入背包已装入物品的总重量
load += weights[i];
// 当前物品无法完整放入,将物品编号和可放物品比例放入组合方案中
compose.push({ id: i, dart: true, scale: r });
}
}
// 返回物品总价值
return { val: val, compose: compose };
}
编写测试代码
我们用一开始的例子,测试下上述代码是否正确执行。
const designSkills = new DesignSkills();
const values = [3, 4, 5],
weights = [2, 3, 4],
capacity = 6;
console.log("容量为6的背包其解决方案为:", designSkills.knapSackGreedy(capacity, weights, values));
回溯算法
回溯是一种渐进式寻找并构建问题解决方式的策略,我们会从一个可能的动作开始试着用这个动作解决问题。如果不能解决,就回溯选择另一个动作直到问题解决。
回溯算法会尝试所有可能的动作(如果更快找到了解决办法就尝试较少的次数)来解决问题。
实例讲解
接下来我们通过两个例子来讲解下回溯算法。
迷宫老鼠问题
迷宫老鼠问题的规则如下:
- 给定一个大小为
N*N的矩阵,矩阵的每个位置都是一个方块。 - 每个位置的值为0或1
- 0表示这个格子有障碍物不能走,1表示这个格子为空闲状态可以走
如下表所示为一个矩阵,其中S是起点,D是重点
| S | |||
|---|---|---|---|
| D |
矩阵就是迷宫,老鼠的目标就是从S位置移动到D位置,老鼠可以在垂直或水平方向上任意值为1的格子间移动。
接下来,我们来看一个具体的例子,下表描述了一个迷宫:
| M | 0 | 1 | 2 | 3 |
|---|---|---|---|---|
| 0 | 1 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 | 1 |
| 2 | 0 | 0 | 1 | 0 |
| 3 | 0 | 1 | 1 | 1 |
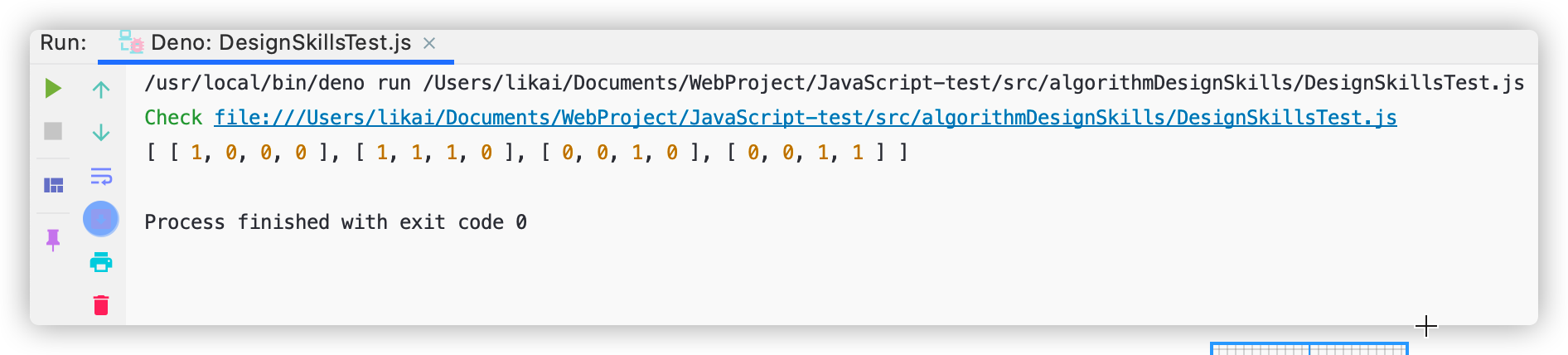
只有格子为1时,老鼠才能移动,所以上述迷宫老鼠移动轨迹为:[0][0] -> [1][0] -> [1][1] -> [1][2] -> [2]][2] -> [3][2] -> [3][3]
实现思路
上述迷宫的老鼠运动轨迹是经过大脑+眼睛+手配合得出的解决方案,那么如何利用回溯算法来得出上述答案?接下来我们就来看下其实现思路。
判断格子是否可走会用到递归,因此该算法分为2部分,我们先来看看算法的主体实现
- 接收一个参数
maze,其类型为一个二维数组,表示迷宫主体。 - 声明辅助变量
solution,用于存放解决方案 - 初始化
solution,将所有格子填充为o - 从起始位置
[0][0]开始寻找路径,更新solution - 寻找路径方法返回
true则返回solution,否则返回无解
再然后,我们来看看寻找路径的递归函数的实现
- 寻找路径函数接收4个参数:横纵坐标
x, y、迷宫maze、解决方案solution - 由于该函数为递归实现,因此我们先确立递归的基准条件:当x和y都到终点时。即:
x = n-1 && y = n-1,满足条件时,我们将解决方案的最后一个位置标为1然后返回解决方案 - 判断迷宫
x,y位置的值是否可走,判断条件为:x和y的值必须大于等于0且x和y的值必须必须小于迷宫的长度且x,y位置的值不为0 - 如果可以走,则将
solution该格子的值改为1 - 随后,老鼠的位置向下移动一格,即
x+1,用新的值递归调用寻找路径函数 - 向下移动的过程中,如果遇到格子的值为0时,则向右移动老鼠的位置,即
y+1,用新的值递归调用寻找路径函数。 - 上述两个条件都无法满足,则表示老鼠水平和垂直都不能移动,则将该格子的值改为0,表示无法移动,回溯,即将当前层从递归栈中移除,寻找另一种解决方案。
- 当所有方案都尝试完毕后还是未能找到解,则代表该迷宫无解,返回false。
接下来,我们把上述实现思路应用到一开始我们举的例子中,最终构成的解决方案如下表所示。
| S | 0 | 1 | 2 | 3 |
|---|---|---|---|---|
| 0 | 1 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 | 0 |
| 2 | 0 | 0 | 1 | 0 |
| 3 | 0 | 0 | 1 | 1 |
实现代码
接下来,我们将上述思路转换为代码。
/**
* 回溯算法:迷宫老鼠问题
*
* @param maze 迷宫
*/
ratInAmaze(maze: number[][]): number[][] | string {
// 解决方案
const solution: number[][] = [];
for (let i = 0; i < maze.length; i++) {
solution[i] = [];
for (let j = 0; j < maze[i].length; j++) {
solution[i][j] = 0;
}
}
// 寻找路径
if (this.findPath(0, 0, maze, solution)) {
// 返回解决方案
return solution;
}
// 无解
return "此迷宫无解";
}
// 寻找路径
findPath(x: number, y: number, maze: number[][], solution: number[][]): boolean {
const n = maze.length;
// 递归基准条件:老鼠走到了迷宫的尽头
if (x === n - 1 && y === n - 1) {
// 将最后一个位置标记为路径的一部分
solution[x][y] = 1;
return true;
}
// 判断老鼠能否安全移动到该位置
if (this.isSafe(maze, x, y)) {
// 该位置可以移动,将其标注为可移动
solution[x][y] = 1;
// 沿着迷宫的行移动
if (this.findPath(x + 1, y, maze, solution)) {
return true;
}
// 沿着迷宫的列移动
if (this.findPath(x, y + 1, maze, solution)) {
return true;
}
// 水平和垂直都无法移动,将这步路径标注为不可移动
solution[x][y] = 0;
// 回溯,即将当前层从递归栈中移除,尝试另一种解决方案
return false;
}
// 所有移动方案都尝试完毕,都无法移动,则退出当前递归
return false;
}
// 验证此位置是否能走
isSafe(maze: number[][], x: number, y: number): boolean {
const n = maze.length;
// x和y必须大于等于0且迷宫的第x行y列不能为0老鼠就可以走
return x >= 0 && y >= 0 && x < n && y < n && maze[x][y] !== 0;
}
编写测试代码
const designSkills = new DesignSkills();
// 迷宫老鼠问题
const RatResult = designSkills.ratInAmaze([
[1, 0, 0, 0],
[1, 1, 1, 1],
[0, 0, 1, 0],
[0, 1, 1, 1]
]);
console.log(RatResult);
数独解题器
数独的游戏规则如下:
- 由一个
9*9的矩阵组成 - 矩阵的每行每列都由
1~9这9个数字组成,且不重复 - 矩阵中还包含了
3*3的小矩阵,同样由9个数字组成,且不重复。 - 游戏开始前会提供一个数独矩阵,它填充了部分数字,未填充部分用0表示
我们通过一个例子来讲解下,如下表所示,准备了一个数独,它填充了部分数字。
| S | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 5 | 3 | 7 | ||||||
| 1 | 6 | 1 | 9 | 5 | |||||
| 2 | 9 | 8 | 6 | ||||||
| 3 | 8 | 6 | 3 | ||||||
| 4 | 4 | 8 | 3 | 1 | |||||
| 5 | 7 | 2 | 6 | ||||||
| 6 | 6 | 2 | 8 | ||||||
| 7 | 4 | 1 | 9 | 5 | |||||
| 8 | 8 | 7 | 9 |
我们根据上述规则,将剩余格子填充,填充好的数独如下所示:
| S | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 5 | 3 | 4 | 6 | 7 | 8 | 9 | 1 | 2 |
| 1 | 6 | 7 | 2 | 1 | 9 | 5 | 3 | 4 | 8 |
| 2 | 1 | 9 | 8 | 3 | 4 | 2 | 5 | 6 | 7 |
| 3 | 8 | 5 | 9 | 7 | 6 | 1 | 4 | 2 | 3 |
| 4 | 4 | 2 | 6 | 8 | 5 | 3 | 7 | 9 | 1 |
| 5 | 7 | 1 | 3 | 9 | 2 | 4 | 8 | 5 | 6 |
| 6 | 9 | 6 | 1 | 5 | 3 | 7 | 2 | 8 | 4 |
| 7 | 2 | 6 | 7 | 4 | 1 | 9 | 6 | 3 | 5 |
| 8 | 3 | 4 | 5 | 2 | 8 | 6 | 1 | 7 | 9 |
实现思路
接下来,我们根据上述规则,来看下如何将其实现。
由于是回溯问题,因此我们需要用到递归,我们先来看看算法的主体实现。
- 接收一个参数
matrix,即数独。 - 调用递归函数,填充数独。
- 如果递归函数将数独填充完毕,则返回填充好的数独。否则返回错无解。
我们来看看递归函数的实现。
- 接收一个参数
matrix,即待填充的数独 - 我们声明三个辅助变量
row, col, checkBankSpaces分别用于描述数独的行、列、当前格子是否为空 - 遍历数独,寻找空格子,记录空格子的位置,即:
row, col - 递归基线条件:格子不为空
- 为空格子填充数字,判断其是否满足数独的填充规则
- 如果满足规则就往空格子填充对应的数字
- 继续递归,寻找空格子进行填充
- 所有数字都尝试完后,仍然不满足规则,就填充0
- 回溯,返回上一个递归栈
检查值是否满足填充规则的条件如下:
- 当前填充的数字在其行中不重复
- 当前填充的数字在其列中不重复
- 当前填充的数字在其
3*3的矩阵中不重复
实现代码
接下来,我们将上述实现思路转换为代码。
/**
* 数独解题器
* 游戏规则:
* 1. 用数字1~9填满一个9*9的矩阵
* 2. 矩阵的每行每列都由1~9这九个数字组成,且不能重复
* 3. 矩阵还包含了3*3的小矩阵,同样需要用这9个数字填满,填充时其值所在的小矩阵中不能有重复的数字
* 4. 游戏开始前会提供一个数独矩阵,它填了部分数字,未填充部分用0表示
* @param matrix 数独矩阵
*/
sudokuSolver(matrix: number[][]): number[][] | string {
if (this.solveSudoku(matrix)) {
return matrix;
}
return "此问题无解";
}
/**
* 解数独
* @param matrix 数独
* @private
*/
private solveSudoku(matrix: number[][]) {
// 辅助变量用于描述数独的行和列
let row: number;
let col = 0;
// 检查格子是否为空
let checkBlankSpaces = false;
// 寻找空格子
for (row = 0; row < matrix.length; row++) {
for (col = 0; col < matrix[row].length; col++) {
// 检测到空格子,终止内层循环
if (matrix[row][col] === this.UNASSIGNED) {
checkBlankSpaces = true;
break;
}
}
// 格子为空终止外层循环
if (checkBlankSpaces) {
break;
}
}
// 格子不为空时终止递归
if (!checkBlankSpaces) {
return true;
}
// 为空格子填充数字,判断其是否满足数独的填充规则
for (let num = 1; num <= 9; num++) {
// 如果满足规则,就往空格子填充num
if (DesignSkills.MatrixIsSafe(matrix, row, col, num)) {
matrix[row][col] = num;
// 递归,继续寻找空格子,然后填充
if (this.solveSudoku(matrix)) {
return true;
}
// 所有数字都尝试完后,仍然不满足则填充0
matrix[row][col] = this.UNASSIGNED;
}
}
// 回溯,即将返回到上一个递归栈
return false;
}
/**
* 校验当前值是否冲突
* @param matrix
* @param row
* @param col
* @param num
* @private
*/
private static MatrixIsSafe(matrix: number[][], row: number, col: number, num: number): boolean {
// 当num的值不再当前行,不在当前列,不在3*3的小格子中时则表示num不冲突
return (
!DesignSkills.usedInRow(matrix, row, num) &&
!DesignSkills.usedInCol(matrix, col, num) &&
!DesignSkills.usedInBox(matrix, row - (row % 3), col - (col % 3), num)
);
}
/**
* 检测当前值是否在矩阵的指定行中
* @param matrix
* @param row
* @param num
* @private
*/
private static usedInRow(matrix: number[][], row: number, num: number): boolean {
for (let col = 0; col < matrix.length; col++) {
if (matrix[row][col] === num) {
return true;
}
}
return false;
}
/**
* 检测当前值是否在矩阵的指定列中
* @param matrix
* @param col
* @param num
* @private
*/
private static usedInCol(matrix: number[][], col: number, num: number): boolean {
for (let row = 0; row < matrix.length; row++) {
if (matrix[row][col] === num) {
return true;
}
}
return false;
}
/**
* 检测当前值是否在3*3的小矩阵中
* @param matrix
* @param boxStartRow
* @param boxStartCol
* @param num
* @private
*/
private static usedInBox(matrix: number[][], boxStartRow: number, boxStartCol: number, num: number): boolean {
for (let row = 0; row < 3; row++) {
for (let col = 0; col < 3; col++) {
if (matrix[row + boxStartRow][col + boxStartCol] === num) {
return true;
}
}
}
return false;
}
编写测试代码
const designSkills = new DesignSkills();
// 数独解题器
const sudokuGrid = [
[5, 3, 0, 0, 7, 0, 0, 0, 0],
[6, 0, 0, 1, 9, 5, 0, 0, 0],
[0, 9, 8, 0, 0, 0, 0, 6, 0],
[8, 0, 0, 0, 6, 0, 0, 0, 3],
[4, 0, 0, 8, 0, 3, 0, 0, 1],
[7, 0, 0, 0, 2, 0, 0, 0, 6],
[0, 6, 0, 0, 0, 0, 2, 8, 0],
[0, 0, 0, 4, 1, 9, 0, 0, 5],
[0, 0, 0, 0, 8, 0, 0, 7, 9]
];
console.log(designSkills.sudokuSolver(sudokuGrid));

写在最后
- 文中如有错误,欢迎在评论区指正,如果这篇文章帮到了你,欢迎点赞和关注😊
- 本文首发于掘金,未经许可禁止转载💌



评论区